题目内容
已知二次函数f(x)=ax2+bx+c,f(2)=0,f(-5)=0,f(0)=1,求这个二次函数.
考点:二次函数的性质
专题:函数的性质及应用
分析:将三点分别代入一般式,然后解方程组即可解决.
解答:
解:∵y=ax2+bx+c满足f(2)=0,f(-5)=0,f(0)=1,
即经过A(2,0),B(-5,0),C(0,1)三点,
∴
,
解得:
,
因此,这个二次函数的解析式是f(x)=-
x2-
x+1.
即经过A(2,0),B(-5,0),C(0,1)三点,
∴
|
解得:
|
因此,这个二次函数的解析式是f(x)=-
| 1 |
| 10 |
| 3 |
| 10 |
点评:此题主要考查了待定系数法求二次函数解析式,题目比较简单.

练习册系列答案
相关题目
等差数列{an}中,a1=1,a4=7,则数列{an}的公差为( )
| A、1 | B、2 | C、3 | D、4 |
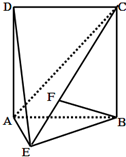 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.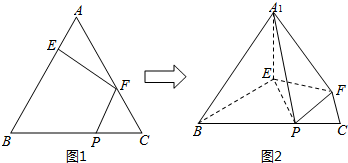
 如图所示,在⊙O上半圆中,AC=a,CB=b,CD⊥AB,EO⊥AB,请你利用CD≤OD≤CE写出一个含有a,b的不等式
如图所示,在⊙O上半圆中,AC=a,CB=b,CD⊥AB,EO⊥AB,请你利用CD≤OD≤CE写出一个含有a,b的不等式