Question

点（

2

，2）与点（-2，-

1

2

）分别在幂函数f（x），g（x）的图象上，问：当x为何值时，有：
①f（x）＞g（x）？
②f（x）=g（x）？
③f（x）＜g（x）？

Answer 1

考点：幂函数的性质

专题：函数的性质及应用

分析：利用幂函数的定义可得f（x）=x²，g（x）=

1

x

．结合图象即可得出．

解答： 解：设f（x）=x^α，g（x）=x^β，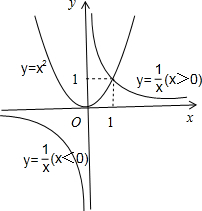
∵点（

2

，2）与点（-2，-

1

2

）分别在幂函数f（x），g（x）的图象上，
∴2=(

2

)α，-

1

2

=(-2)β，
解得α=2，β=-1．
∴f（x）=x²，g（x）=

1

x

．
①由f（x）＞g（x），可得x2＞

1

x

，
当x＜0时，上式成立；当x＞0时，化为x³＞1，∴x＞1．
综上可得：当x＜0或x＞1时，f（x）＞g（x）．
②由f（x）=g（x），可得x³=1，解得x=1．
∴当x=1时，f（x）=g（x）．
③由f（x）＜g（x），可得x2＜

1

x

，
必须x＞0，化为x³＜1，解得0＜x＜1．
∴当0＜x＜1时，f（x）＜g（x）．

点评：本题考查了幂函数的定义图象与性质，属于基础题．