题目内容
已知二面角α-AB-β的平面角是锐角θ，α内一点C到β的距离为3，点C到棱AB的距离为4，那么tanθ的值等于（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：二面角的平面角及求法
专题：空间角
分析：根据已知条件作出图形，根据图形即可找到角θ，根据已知的边的长度即可求出tanθ．
解答：
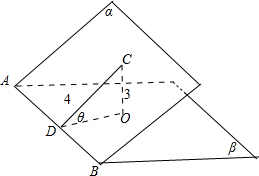解：如图所示，CO⊥β，垂足为O，CD⊥AB，垂足为D，且CO=3，CD=4，连接DO，
∵CO⊥β，∴CO⊥DO，
∴在Rt△CDO中，DO=
；
∵CO⊥β，AB?β，
∴CO⊥AB，即AB⊥CO，又AB⊥CD，CD∩CO=C；
∴AB⊥平面CDO，DO?平面CDO，∴AB⊥DO；
∴∠CDO是二面角α-AB-β的平面角，∴∠CDO=θ；
∴tanθ=
=
=
．
故选D．
解：如图所示，CO⊥β，垂足为O，CD⊥AB，垂足为D，且CO=3，CD=4，连接DO，∵CO⊥β，∴CO⊥DO，
∴在Rt△CDO中，DO=
| 7 |
∵CO⊥β，AB?β，
∴CO⊥AB，即AB⊥CO，又AB⊥CD，CD∩CO=C；
∴AB⊥平面CDO，DO?平面CDO，∴AB⊥DO；
∴∠CDO是二面角α-AB-β的平面角，∴∠CDO=θ；
∴tanθ=
| CO |
| DO |
| 3 | ||
|
3
| ||
| 7 |
故选D．
点评：考查二面角以及二面角的平面角的概念，而借助图形会比较形象的求解本题，以及线面垂直的判定定理．
练习册系列答案
相关题目
设Sn为等比数列{an}的前n项和，若
=8，则
=（ ）
| a6 |
| a3 |
| S6 |
| S3 |
| A、8 | B、9 | C、15 | D、16 |
在复平面内，复数1-3i，（1+i）（2-i）对应的点分别为A、B，则线段AB的中点C对应的复数为（ ）
| A、-4+2i | B、4-2i |
| C、-2+i | D、2-i |
集合M={x|（x+2）（x-2）≤0}，N={x|-1＜x＜3}，则M∩N=（ ）
| A、{ x|-1≤x＜2} |
| B、{ x|-1＜x≤2} |
| C、{ x|-2≤x＜3} |
| D、{ x|-2＜x≤2} |