题目内容
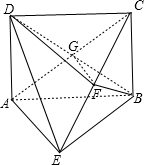
 如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC、BD交于点G.
如图,矩形ABCD中,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE,AC、BD交于点G.(1)求证:AE⊥平面BCE;
(2)求点C到平面BDF的距离.
考点:点、线、面间的距离计算,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)根据已知条件先证明BC⊥平面ABE,进一步利用BF⊥平面ACE得到:BF⊥AE,最后证明AE⊥平面BCE.
(2)要求点C到平面BDF的距离,首先证明CF⊥平面BFG,然后根据线段之间的关系求的结果
(2)要求点C到平面BDF的距离,首先证明CF⊥平面BFG,然后根据线段之间的关系求的结果
解答:
(1)证明:∵四边形ABCD是矩形,
∴BC∥AD
∵AD⊥平面ABE
∴BC⊥平面ABE
∵BF⊥平面ACE
∴BF⊥AE
∴AE⊥平面BCE
(2)解:∵AE=EB=BC=2且BF⊥平面ACE
∴F是EC的中点,
∴GF∥AE
∴GF⊥CE
又BF⊥CE
∴CF⊥平面BFG
点C到平面BDF的距离:即CF
∵EB=BC=2
∵EC2=BE2+BC2=8
利用勾股定理得:CF=
EC=
∴BC∥AD
∵AD⊥平面ABE
∴BC⊥平面ABE
∵BF⊥平面ACE
∴BF⊥AE
∴AE⊥平面BCE
(2)解:∵AE=EB=BC=2且BF⊥平面ACE
∴F是EC的中点,
∴GF∥AE
∴GF⊥CE
又BF⊥CE
∴CF⊥平面BFG
点C到平面BDF的距离:即CF
∵EB=BC=2
∵EC2=BE2+BC2=8
利用勾股定理得:CF=
| 1 |
| 2 |
| 2 |

点评:本题考查的知识要点:线面垂直的性质定理和判定定理,点到平面的距离及相关的运算问题.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
集合M={x|(x+2)(x-2)≤0},N={x|-1<x<3},则M∩N=( )
| A、{ x|-1≤x<2} |
| B、{ x|-1<x≤2} |
| C、{ x|-2≤x<3} |
| D、{ x|-2<x≤2} |
设x∈R,则“x<-1”是“2x2+x-1>0”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |