题目内容
已知f(x)=
cos2x-sin2x,若y=f(x-m)(m>0)是奇函数,则m的最小值为( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:两角和与差的正弦函数
专题:三角函数的图像与性质
分析:利用三角恒等变换的应用可得f(x)=2cos(2x+
),于是得f(x-m)=2cos[2(x-m)+
],利用y=f(x-m)(m>0)是奇函数,可得答案.
| π |
| 6 |
| π |
| 6 |
解答:
解:∵f(x)=
cos2x-sin2x=2(
cos2x-
sin2x)=2cos(2x+
),
∴y=f(x-m)=2cos[2(x-m)+
],
∵y=f(x-m)(m>0)是奇函数,
∴
-2m=kπ+
(k∈Z),
∴2m=-kπ-
(k∈Z),又m>0,
显然,k=-1时,m得到最小值,为
.
故选:C.
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∴y=f(x-m)=2cos[2(x-m)+
| π |
| 6 |
∵y=f(x-m)(m>0)是奇函数,
∴
| π |
| 6 |
| π |
| 2 |
∴2m=-kπ-
| π |
| 3 |
显然,k=-1时,m得到最小值,为
| π |
| 3 |
故选:C.
点评:本题考查三角恒等变换的应用,考查余弦函数的性质,突出正弦与余弦奇偶性转化的考查,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在一次防恐演习中,某射手击中目标的概率为0.8,每次射击的结果相互独立,现射击99次,则他最有可能射中目标( )次.
| A、99 | B、80 |
| C、79或80 | D、79 |
已知集合A={x|y=
},B={y|y=2x,x∈R},则A∩B=( )
| x-x2 |
| A、[0,1] |
| B、(0,1) |
| C、(0,1] |
| D、[0,1) |
在复平面内,复数
-i3对应的点位于( )
| 2 |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
在区间[-1,1]内随机取两个实数x,y,则满足y≥x2-1的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=ax2+bx+c(a,b,c∈R,a<0)对于一切实数x都有f(1-x)=f(1+x),而且f(-1)<0,f(0)>0,则有( )
| A、a+b+c<0 |
| B、c<2b |
| C、abc>0 |
| D、b<a+c |
已知
sin(π-2x)-1=cos2x(0<x<π),则tan2x的值是( )
| 1 |
| 2 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
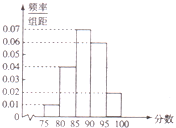 某校高三有800名同学参加学校组织的数学学科竞赛,其成绩的频率分布直方图如图所示,规定95分及其以上为一等奖.
某校高三有800名同学参加学校组织的数学学科竞赛,其成绩的频率分布直方图如图所示,规定95分及其以上为一等奖.