题目内容
已知
sin(π-2x)-1=cos2x(0<x<π),则tan2x的值是( )
| 1 |
| 2 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:首先,借助于诱导公式和二倍角公式,化简得到tanx=2,然后,利用二倍角的正切公式进行求解.
解答:
解:∵
sin(π-2x)-1=cos2x,
∴
sin2x-1=cos2x,
∴
sin2x=1+cos2x=2cos2x,
∴sinxcosx=2cos2x,
∴tanx=2,
∴tan2x=
,
=
=-
,
∴tan2x的值是-
.
故选:A.
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴sinxcosx=2cos2x,
∴tanx=2,
∴tan2x=
| 2tanx |
| 1-tan2x |
=
| 2×2 |
| 1-22 |
| 4 |
| 3 |
∴tan2x的值是-
| 4 |
| 3 |
故选:A.
点评:本题重点考查了二倍角公式、诱导公式等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某简单组合体的三视图如图所示,则该组合体的体积为( )
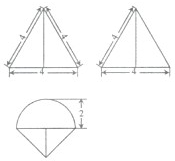

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知复数z=2+i,
是z的共轭复数,则
对应的点位于( )
. |
| z |
| ||
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知f(x)=
cos2x-sin2x,若y=f(x-m)(m>0)是奇函数,则m的最小值为( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=2sin(2x+
)的一条对称轴是( )
| π |
| 6 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
已知A={x|log2x<2},B={x|
<3x<
},则A∩B为( )
| 1 |
| 3 |
| 3 |
A、(0,
| ||
B、(0,
| ||
C、(-1,
| ||
D、(-1,
|
在(2
-
)5的二项展开式中,x的系数为( )
| x |
| 1 |
| x |
| A、-80 | B、-5 | C、10 | D、80 |
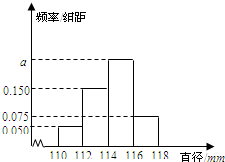 某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112],[112,114],[114,116],[116,118]内该厂可获利分别为10,20,30,10(单位:元),现从该厂生产的产品A中随机100件测量它们的直径,得到如图所示的频率分布直方图.
某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112],[112,114],[114,116],[116,118]内该厂可获利分别为10,20,30,10(单位:元),现从该厂生产的产品A中随机100件测量它们的直径,得到如图所示的频率分布直方图.