题目内容
已知x2-3x+1=0，求x3+
的值．
| 1 |
| x3 |
考点：二次函数的性质
专题：计算题
分析：将已知条件进行变形，得到：x+
=3，x2+
=7，再利用立方和公式展开代入求出即可．
| 1 |
| x |
| 1 |
| x2 |
解答：
解：∵x2-3x+1=0，
∴x+
=3，
∴x2+
=9-2=7，
∴x3+
=（x+
）（x2-1+
）
=3×（7-1）
=18．
∴x+
| 1 |
| x |
∴x2+
| 1 |
| x2 |
∴x3+
| 1 |
| x3 |
| 1 |
| x |
| 1 |
| x2 |
=3×（7-1）
=18．
点评：本题考察了等式的变形问题，以及立方和公式的展开式，本题是一道基础题．
练习册系列答案
相关题目
已知f（x）=
cos2x-sin2x，若y=f（x-m）（m＞0）是奇函数，则m的最小值为（ ）
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
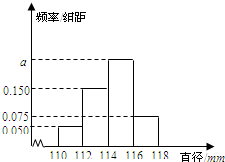某工厂生产的产品A的直径均位于区间[110，118]内（单位：mm）．若生产一件产品A的直径位于区间[110，112]，[112，114]，[114，116]，[116，118]内该厂可获利分别为10，20，30，10（单位：元），现从该厂生产的产品A中随机100件测量它们的直径，得到如图所示的频率分布直方图．