题目内容
用区间表示集合{x|x＞-1且x≠2}= ．
考点：区间与无穷的概念
专题：计算题,函数的性质及应用
分析：给出的集合是大于0且不等于2的所有实数构成的，只要写出两个开区间的并集即可．
解答：
解：集合{x|x＞0且x≠2}用区间表示为：
（0，2）∪（2，+∞）．
故答案为：（0，2）∪（2，+∞）．
（0，2）∪（2，+∞）．
故答案为：（0，2）∪（2，+∞）．
点评：本题考查了区间与无穷的概念，考查了集合与区间的等价转换，是基础题．
练习册系列答案
相关题目
如果圆x2+y2+Dx+Ey+F=0与x轴相切于原点，则（ ）
| A、E≠0，D=F=0 |
| B、D≠0，E≠0，F=0 |
| C、D≠0，E=F=0 |
| D、F≠0，D=E=0 |
如图，点P（m，1）是双曲线y=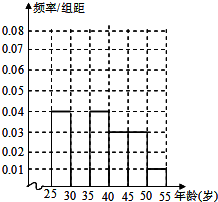
某高中社团进行社会实践，对[25，55]岁的人群随机抽取n人进行了一次是否开通“微博”的调查，若开通“微博”的称为“时尚族”，否则称为“非时尚族”．通过调查分别得到如图所示统计表，如图2所示各年龄段人数频率分布直方图．