Question

已知由不等式组

x≤0 y≥0 y-kx≤2 y-x-4≤0

，确定的平面区域Ω的面积为7，定点M的坐标为（1，-2），若N∈Ω，O为坐标原点，则

OM

•

ON

的最小值是（　　）

• A、-8
• B、-7
• C、-6
• D、-4

Answer 1

考点：简单线性规划

专题：数形结合,不等式的解法及应用,平面向量及应用

分析：首先作出不等式组

x≤0 y≥0 y-x-4≤0

所表示的平面区域，然后根据直线y=kx+2恒过点B（0，2），且原点的坐标恒满足y-kx≤2，当k=0时，y≤2，此时平面区域Ω的面积为6，由于6＜7，由此可得k＜0．联立方程组求出D的坐标，根据三角形的面积公式求得k的值，最后把

OM

•

ON

转化为线性目标函数解决．

解答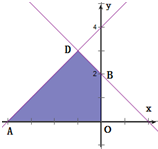： 解：依题意画出不等式组

x≤0 y≥0 y-x-4≤0

所表示的平面区域（如右图所示）
可知其围成的区域是等腰直角三角形面积为8，
由直线y=kx+2恒过点B（0，2），且原点的坐标恒满足y-kx≤2，
当k=0时，y≤2，此时平面区域Ω的面积为6，
由于6＜7，由此可得k＜0．
由

y-kx=2 y-x-4=0

可得D(

2

k-1

，

4k-2

k-1

)，
依题意应有

1

2

×2×|

2

k-1

|=1，因此k=-1（k=3，舍去）．
故有D（-1，3），
设N（x，y），
由z=

OM

•

ON

=x-2y，可化为y=

1

2

x-

1

2

z，
∵

1

2

＜1，
∴当直线y=

1

2

x-

1

2

z过点D时，截距-

1

2

z最大，即z取得最小值-7．
故选：B．

点评：本题考查了简单的线性规划，考查了数形结合的解题思想方法和数学转化思想方法，考查了平面向量的数量积的运用，是中档题．