题目内容
12.2cos275°-1的值为( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | -$\frac{{\sqrt{3}}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
分析 直接利用二倍角的余弦,求得要求式子的值.
解答 解:2cos275°-1=cos150°=-cos30°=-$\frac{\sqrt{3}}{2}$,
故选:B.
点评 本题主要考查二倍角的余弦的应用,属于基础题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
3.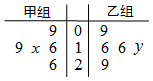 如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x、y的值分别为( )
如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x、y的值分别为( )
 如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x、y的值分别为( )
如图所示茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为17,乙组数据的平均数为17.4,则x、y的值分别为( )| A. | 7、8 | B. | 5、7 | C. | 8、5 | D. | 7、7 |
17.数列{an}满足a1=2,a2=1,并且$\frac{{a}_{n}}{{a}_{n-1}}$+$\frac{{a}_{n}}{{a}_{n+1}}$=2(n≥2),则数列{an}的第100项为( )
| A. | $\frac{1}{{{2^{100}}}}$ | B. | $\frac{1}{{{2^{50}}}}$ | C. | $\frac{1}{100}$ | D. | $\frac{1}{50}$ |
4.若a,b∈R,i是虚数单位,且b+(a-1)i=1+i,则a+b的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
1.已知i为虚数单位,若复数$z=\frac{1-ti}{1+i}$在复平面内对应的点在第四象限,则t的取值范围为( )
| A. | [-1,1] | B. | (-1,1) | C. | (-∞,-1) | D. | (1,+∞) |
2.某校开设A类选修课3门和B类选修课4门,一位同学从中任选3门,则两类课程都有选的概率为( )
| A. | $\frac{6}{7}$ | B. | $\frac{5}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{1}{7}$ |
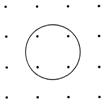 如图所示,在排成4×4方阵的16个点中,中心位置4个点在某圆内,其余12个点在圆外.从16个点中任选3点,作为三角形的顶点,其中至少有一个顶点在圆内的三角形共有312个.
如图所示,在排成4×4方阵的16个点中,中心位置4个点在某圆内,其余12个点在圆外.从16个点中任选3点,作为三角形的顶点,其中至少有一个顶点在圆内的三角形共有312个.