题目内容
2．
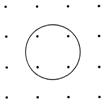如图所示，在排成4×4方阵的16个点中，中心位置4个点在某圆内，其余12个点在圆外．从16个点中任选3点，作为三角形的顶点，其中至少有一个顶点在圆内的三角形共有312个．
分析 根据题意，按圆内取出的点的数目分3种情况讨论：①、取出的3个点都在圆内，②、在圆内取2点，圆外12点中取1点，③、在圆内取1点，圆外12点中取2点，分别求出每一种情况的取法数目，由分类计数原理计算可得答案．
解答 解：根据题意，分3种情况讨论：
①、取出的3个点都在圆内，有C43=4种取法，即有4种取法，
②、在圆内取2点，圆外12点中取1点，有C42C101=60种，即有60种取法，
③、在圆内取1点，圆外12点中取2点，有C41（C122-4）=248种，即有248种取法，
则至少有一个顶点在圆内的三角形有4+60+248=312个，
故答案为：312．
点评 本题考查排列、组合的实际应用，注意要分类讨论，要做到不重不漏．
练习册系列答案
相关题目
12．观察下列各式：1=12，2+3+4=32，3+4+5+6=52，4+5+6+7+8+9+10=72，…，可以得出的一般结论是（ ）
| A． | n+（n+1）+（n+2）+…+（3n-2）=n2 | B． | n+（n+1）+（n+2）+…+（3n-2）=（2n-1）2 | ||
| C． | n+（n+1）+（n+2）+…+（3n-1）=n2 | D． | n+（n+1）+（n+2）+…+（3n-1）=（2n-1）2 |
10．已知数列{an}中，a3=2，a7=1，若数列$\left\{{\frac{1}{{1+{a_n}}}}\right\}$是等差数列，则a11等于（ ）
| A． | 0 | B． | $\frac{1}{3}$ | C． | $\frac{1}{6}$ | D． | $\frac{1}{2}$ |
7．已知向量$\vec a=（1，2）$，$\vec b=（1，0）$，$\vec c=（3，4）$．若λ为实数，$（\overrightarrow a+λ\overrightarrow b）∥\overrightarrow c$，则λ=（ ）
| A． | 2 | B． | 1 | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |
12．2cos275°-1的值为（ ）
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | -$\frac{{\sqrt{3}}}{2}$ | C． | -$\frac{1}{2}$ | D． | $\frac{1}{2}$ |