题目内容
已知向量
，
是夹角为60°的单位向量．当实数λ≤-1时，向量
与向量
+λ
的夹角范围是（ ）
| a |
| b |
| a |
| a |
| b |
| A、[0°，60°） |
| B、[60°，120°） |
| C、[120°，180°） |
| D、[60°，180°） |
考点：数量积表示两个向量的夹角
专题：平面向量及应用
分析：根据向量的几何意义，画出图形，结合图形得出向量
与向量
+λ
的夹角范围是什么．
| a |
| a |
| b |
解答：
解：∵向量
，
是夹角为60°的单位向量，
∴画出图形，如图所示；
设
=
，
=
，∠AOB=60°，
当λ=-1时，
+λ
=
+
=
，
此时
与
+λ
的夹角为∠AOD=60°；
当λ＜-1时，
+λ
=
+
=
，
此时
与
+λ
的夹角为∠AOF，
且∠AOD＜∠AOF＜∠AOE；
综上，向量
与向量
+λ
的夹角范围是[60°，120°）．
故选：B．
| a |
| b |
∴画出图形，如图所示；
设
| OA |
| a |
| OB |
| b |
当λ=-1时，
| a |
| b |
| OA |
| OC |
| OD |
此时
| a |
| a |
| b |
当λ＜-1时，
| a |
| b |
| OE |
| OA |
| OF |
此时
| a |
| a |
| b |
且∠AOD＜∠AOF＜∠AOE；
综上，向量
| a |
| a |
| b |
故选：B．
点评：本题考查了平面向量的加法与减法运算的几何意义的应用问题，是基础题目．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
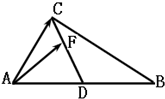如图所示，在△ABC中，D为AB的中点，F在线段CD上，设| AB |
| a |
| AC |
| b |
| AF |
| a |
| b |
| 1 |
| x |
| 2 |
| y |
A、8+2
| ||
| B、8 | ||
| C、6 | ||
D、6+2
|