题目内容
画出函数y=
的图象,并写出作图步骤.
| 1 |
| x2-1 |
考点:函数图象的作法
专题:函数的性质及应用
分析:由条件根据函数的定义域、值域、单调性、图象的对称性,列表连线作出函数的图象.
解答:
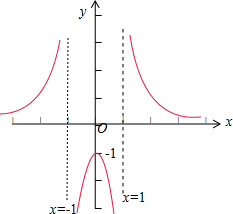 解:函数y=
解:函数y=
的定义域为[x|x≠±1},
当x>1时,函数y在(1,+∞)上单调递减,且y>0.
且当x趋于1时,函数值y趋于正无穷大;当x趋于+∞时,函数值y趋于0.
当x∈[0,1)时,x2-1 单调递增,函数y单调递减,且y≤-1.
根据以上条件,画出函数在[0,+∞)上的图象.
再根据函数为偶函数,它的图象关于y轴对称,即可得到函数y在定义域内的图象.
列表:
描点作图:如图所示:
 解:函数y=
解:函数y=| 1 |
| x2-1 |
当x>1时,函数y在(1,+∞)上单调递减,且y>0.
且当x趋于1时,函数值y趋于正无穷大;当x趋于+∞时,函数值y趋于0.
当x∈[0,1)时,x2-1 单调递增,函数y单调递减,且y≤-1.
根据以上条件,画出函数在[0,+∞)上的图象.
再根据函数为偶函数,它的图象关于y轴对称,即可得到函数y在定义域内的图象.
列表:
| x | -3 | -2 | -
| -
| 0 |
| 2 | 3 | ||||||||||||||
| y |
|
|
| -
| -1 | -
|
|
|
点评:本题主要考查函数的图象的作法,函数的性质应用,属于中档题.

练习册系列答案
相关题目
已知向量
,
是夹角为60°的单位向量.当实数λ≤-1时,向量
与向量
+λ
的夹角范围是( )
| a |
| b |
| a |
| a |
| b |
| A、[0°,60°) |
| B、[60°,120°) |
| C、[120°,180°) |
| D、[60°,180°) |