题目内容
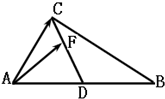 如图所示,在△ABC中,D为AB的中点,F在线段CD上,设
如图所示,在△ABC中,D为AB的中点,F在线段CD上,设| AB |
| a |
| AC |
| b |
| AF |
| a |
| b |
| 1 |
| x |
| 2 |
| y |
A、8+2
| ||
| B、8 | ||
| C、6 | ||
D、6+2
|
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:由D为AB的中点,可得
=2
.由
=x
+y
,可得
=2x
+y
,由F在线段CD上,利用向量共线定理可得2x+y=1.再利用“乘1法”与基本不等式的性质即可得出.
| AB |
| AD |
| AF |
| a |
| b |
| AF |
| AD |
| AC |
解答:
解:∵D为AB的中点,
∴
=2
.
∵
=x
+y
,
∴
=2x
+y
,
∵F在线段CD上,
∴2x+y=1.
又x,y>0.
∴
+
=(2x+y)(
+
)=4+
+
≥4+2
=8,当且仅当y=2x=
时取等号.
∴
+
的最小值为8.
故选:B.
∴
| AB |
| AD |
∵
| AF |
| a |
| b |
∴
| AF |
| AD |
| AC |
∵F在线段CD上,
∴2x+y=1.
又x,y>0.
∴
| 1 |
| x |
| 2 |
| y |
| 1 |
| x |
| 2 |
| y |
| y |
| x |
| 4x |
| y |
|
| 1 |
| 2 |
∴
| 1 |
| x |
| 2 |
| y |
故选:B.
点评:本题考查了向量共线定理、“乘1法”与基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知向量
,
是夹角为60°的单位向量.当实数λ≤-1时,向量
与向量
+λ
的夹角范围是( )
| a |
| b |
| a |
| a |
| b |
| A、[0°,60°) |
| B、[60°,120°) |
| C、[120°,180°) |
| D、[60°,180°) |
已知函数f(x)=x2+1的图象在点A(x1,f(x1))与点B(x2,f(x2))处的切线互相垂直,并交于点P,则点P的坐标可能是( )
A、(
| ||
B、(0,
| ||
| C、(1,3) | ||
D、(1,
|
一个几何体的三视图如图所示,则该几何体的外接球的表面积为( )
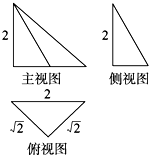

| A、36π | ||
| B、8π | ||
C、
| ||
D、
|