Question

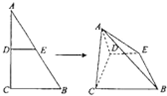如图，直角三角形ABC中，∠ACB=90°，AB=2BC=4，D、E分别为AC、AB边的中点．将△ADE沿DF折起，使二面角A-DE-C的余弦值为

1

3

，求：
（Ⅰ）四棱锥A-BCDE的体积；
（Ⅱ）二面角A-BE-C的余弦值．

Answer 1

考点：用空间向量求平面间的夹角

专题：空间位置关系与距离,空间角

分析：（Ⅰ）由已知得DE⊥AC，DE⊥DC，从而DE⊥平面ADC，进而平面ADC⊥平面CBED，过点A作AM⊥CD，则AM⊥面CBED，由此能求出V_A-BCDE．
（Ⅱ）由已知得ME⊥BE，从而BE⊥平面AME，BE⊥AE，∠AEM为二面角A-BE-C的平面角，由此能求出二面角A-BE-C的余弦值．

解答： 解：（Ⅰ）∵D，E是边AC、AB的中点，
∴DE是△ABC的中位线，
∵直角三角形ABC中，∠ACB=90°，∴DE⊥AC，
∵DE⊥AD，DE⊥DC，AD∩DC=D，
∴DE⊥平面ADC，
∴平面ADC⊥平面CBED，
过点A作AM⊥CD，则AM⊥面CBED，
∵∠ADC为二面角A-DE-C的平面角，∴cos∠ADC=

1

3

，（3分）
AM=

2 6

3

，DM=

3

3

，
∴V_A-BCDE=

1

3

×

2 6

3

×

3 3

2

=

2

．（6分）
（Ⅱ）∵DE=1，DM=

3

3

，∴EM=

2 3

3

，
∵MC=

2 3

3

，BC=2，∴BM=

4 3

3

，BE=2，
BM²=EM²+BE²，∴ME⊥BE，
∵AM⊥BE，AM∩ME=M，
∴BE⊥平面AME，
∴BE⊥AE．（10分）
∴∠AEM为二面角A-BE-C的平面角，
∴cos∠AEM=

MB

AE

=

3

3

．（12分）

点评：本题考查四棱锥的体积的求法，考查二面角的余弦值的求法，解题时要认真审题，注意空间思维能力的培养．