题目内容
| 1 |
| 12+2 |
| 1 |
| 22+4 |
| 1 |
| 32+6 |
| 1 |
| n2+2n |
| 3 |
| 4 |
考点:数列的求和
专题:计算题,等差数列与等比数列
分析:利用裂项法求和,即可得出结论.
解答:
解:
=
=
(
-
),
∴
+
+
+…+
=
(1-
+
-
+…+
-
)=
(1+
-
-
)=
-
,
故答案为:
.
| 1 |
| n2+2n |
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
∴
| 1 |
| 12+2 |
| 1 |
| 22+4 |
| 1 |
| 32+6 |
| 1 |
| n2+2n |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
| 3 |
| 4 |
| n+1 |
| n(n+2) |
故答案为:
| n+1 |
| n(n+2) |
点评:本题考查数列的求和,正确运用裂项法是关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
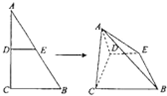 如图,直角三角形ABC中,∠ACB=90°,AB=2BC=4,D、E分别为AC、AB边的中点.将△ADE沿DF折起,使二面角A-DE-C的余弦值为
如图,直角三角形ABC中,∠ACB=90°,AB=2BC=4,D、E分别为AC、AB边的中点.将△ADE沿DF折起,使二面角A-DE-C的余弦值为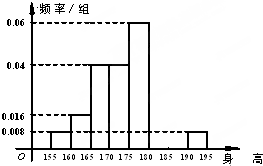 从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.