题目内容
三角形ABC中，角A，B，C所对的边为a，b，c且
+
=2．
（Ⅰ）求A；
（Ⅱ）若a=2，求三角形ABC周长l的最大值．
| bcosC |
| acosA |
| ccosB |
| acosA |
（Ⅰ）求A；
（Ⅱ）若a=2，求三角形ABC周长l的最大值．
考点：正弦定理的应用
专题：三角函数的求值,三角函数的图像与性质,解三角形
分析：（Ⅰ）首先根据三角函数关系式的恒等变换和正弦定理求出A的值
（Ⅱ）由（Ⅰ）的结论和正弦定理进一步通过变换变形成正弦型函数，利用三角函数的单调性求出结果．
（Ⅱ）由（Ⅰ）的结论和正弦定理进一步通过变换变形成正弦型函数，利用三角函数的单调性求出结果．
解答：
解：（Ⅰ）三角形ABC中，角A，B，C所对的边为a，b，c且
+
=2
由正弦定理
=
=
=2R
得：sin2A=sin（B+C）
则：B+C=2A
A=60°
（Ⅱ）由正弦定理：
=
=
b=
sinB c=
sinC
l=2+
sinB+
sinC=2+4（
cosC+
sinC）=2+4sin（C+
）
当C=
时，lmax=6
故答案为：（1）A=60°
（2）当C=
时，lmax=6
| bcosC |
| acosA |
| ccosB |
| acosA |
由正弦定理
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
得：sin2A=sin（B+C）
则：B+C=2A
A=60°
（Ⅱ）由正弦定理：
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
b=
4
| ||
| 3 |
4
| ||
| 3 |
l=2+
4
| ||
| 3 |
4
| ||
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
当C=
| π |
| 3 |
故答案为：（1）A=60°
（2）当C=
| π |
| 3 |
点评：本题考查的知识点：正弦定理，三角关系式的恒等变换，三角形的周长及相关的运算问题．
练习册系列答案
名校课堂系列答案
相关题目
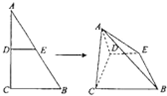如图，直角三角形ABC中，∠ACB=90°，AB=2BC=4，D、E分别为AC、AB边的中点．将△ADE沿DF折起，使二面角A-DE-C的余弦值为
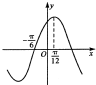如图所示是函数f（x）=sin（?x+φ）（?＞0，|φ|＜π）的部分图象，则f（x）的解析式为