题目内容
集合A={x|x=5k+3，k∈N*}，B={x|x=7k+2，k∈N*}，则A∩B中的最小元素为 ．
考点：交集及其运算
专题：集合
分析：因为随着k的增大，集合A，B中的x都增大，所以让k从1开始取值，依次增大，第一次出现的A∩B的元素便是A∩B中的最小元素．
解答：
解：随着k的增大，x=5k+3，x=7k+2逐渐增大；
k=1，x=8，x=9
k=2，x=13，x=16
k=3，x=18，x=23
k=4，x=23，x=30
∴23是A∩B的元素，且是最小的．
k=1，x=8，x=9
k=2，x=13，x=16
k=3，x=18，x=23
k=4，x=23，x=30
∴23是A∩B的元素，且是最小的．
点评：考查描述法表示集合，函数的单调性，交集的概念．
练习册系列答案
相关题目
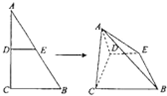如图，直角三角形ABC中，∠ACB=90°，AB=2BC=4，D、E分别为AC、AB边的中点．将△ADE沿DF折起，使二面角A-DE-C的余弦值为