题目内容
设函数f(x)=2ax-
+lnx
(1)当a=-
时,若在[
,2]存在x0,使得不等式f(x0)-c≤0成立,求c的最小值.
(2)若f(x)在(0,+∞)上是单调函数,求a的取值范围.(参考数据e2≈7.389,e3≈20.08)
| a |
| x |
(1)当a=-
| 1 |
| 3 |
| 1 |
| 4 |
(2)若f(x)在(0,+∞)上是单调函数,求a的取值范围.(参考数据e2≈7.389,e3≈20.08)
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)先求出函数的导数,再分别讨论x的取值范围,从而求出c的最小值,
(2)分别讨论a>0,a<0,a=0的情况,从而得出a的范围.
(2)分别讨论a>0,a<0,a=0的情况,从而得出a的范围.
解答:
解:(1)在[
,2]?x0,使不等式f(x0 )-c≤0成立,
只需c≥[f(x)]min,
由f′(x)=-
,
∴x∈[
,
]时,f′(x)<0,
∴f(x)在[
,
]上递减;
当x∈[
,1]时,f′(x)>0,
∴f(x)在[
,1]上递增;
当x∈[1,2]时,f′(x)<0,∴f(x)在[1,2]上递减;
∴f(
)是f(x)在[
,2]上的极小值.
而f(
)=
-ln2,f(2)=-
+ln2,
∴f(
)-f(2)=
-ln4,
又e3-16>0,∴
-ln4>0,
∴[f(x)]min=f(2),
∴c≥[f(x)]min=-
+ln2,
∴c的范围是[-
+ln2,+∞),
∴c的最小值为-
+ln2;
(2)①a=0时,f(x)=lnx,
则f(x)在(0,+∞)递增;
②当a>0时,
∵x>0,∴2ax2+x+a>0,
∴f′x)>0,则f(x)在(0,+∞)递增,
③a<0时,设g(x)=2ax2+x+a,只需△≤0,
从而得a≤-
,此时f(x)在(0,+∞,)递减;
综上得,a的范围是(-∞,-
]∪[0,+∞).
| 1 |
| 4 |
只需c≥[f(x)]min,
由f′(x)=-
| (2x-1)(x-1) |
| 3x2 |
∴x∈[
| 1 |
| 4 |
| 1 |
| 2 |
∴f(x)在[
| 1 |
| 4 |
| 1 |
| 2 |
当x∈[
| 1 |
| 2 |
∴f(x)在[
| 1 |
| 2 |
当x∈[1,2]时,f′(x)<0,∴f(x)在[1,2]上递减;
∴f(
| 1 |
| 2 |
| 1 |
| 4 |
而f(
| 1 |
| 2 |
| 1 |
| 3 |
| 7 |
| 6 |
∴f(
| 1 |
| 2 |
| ln |
e |
又e3-16>0,∴
| ln |
e |
∴[f(x)]min=f(2),
∴c≥[f(x)]min=-
| 7 |
| 6 |
∴c的范围是[-
| 7 |
| 6 |
∴c的最小值为-
| 7 |
| 6 |
(2)①a=0时,f(x)=lnx,
则f(x)在(0,+∞)递增;
②当a>0时,
∵x>0,∴2ax2+x+a>0,
∴f′x)>0,则f(x)在(0,+∞)递增,
③a<0时,设g(x)=2ax2+x+a,只需△≤0,
从而得a≤-
| ||
| 4 |
综上得,a的范围是(-∞,-
| ||
| 4 |
点评:本题考察了函数的单调性,导数的应用,求参数的范围,考察分类讨论思想,是一道综合题.

练习册系列答案
相关题目
 已知 如图,四边形ABCD是等腰梯形,AB∥DC,A(-1,-2),B(6,5),D(0,2).
已知 如图,四边形ABCD是等腰梯形,AB∥DC,A(-1,-2),B(6,5),D(0,2).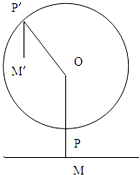 六一儿重节到了,小明与爸爸去游乐场看见了大观览车,已知大观览车轮轴中心为点O,距地面高为32m(即OM=32m),巨轮半径为30m,点p为吊舱与轮的连接点,吊舱高2m(即PM=2m)巨轮每分钟转动30°,小明和爸爸从地面M点进入吊舱后,巨轮开始逆时针转动.
六一儿重节到了,小明与爸爸去游乐场看见了大观览车,已知大观览车轮轴中心为点O,距地面高为32m(即OM=32m),巨轮半径为30m,点p为吊舱与轮的连接点,吊舱高2m(即PM=2m)巨轮每分钟转动30°,小明和爸爸从地面M点进入吊舱后,巨轮开始逆时针转动. 如图,分别写出适合下列条件的角的集合:
如图,分别写出适合下列条件的角的集合: