题目内容
已知二次函数y=f(x)的图象经过点(0,0),其导函数f′(x)=2x-5,当x∈(n+2,n+3](n∈N*)时,函数f(x)值域中整数值的个数记为an.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=(
)an+
(n∈N*),求数列{bn}的前n项和Sn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=(
| 2 |
| 4 |
| a2n-1a2n+1 |
考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)设f(x)=ax2+bx,由其导函数f′(x)=2x-5,得f(x)=x2-5x,由此能求出an=f(n+3)-f(n+2)=2n.
(Ⅱ)bn=(
)an+
(n∈N*)=2n+
(
-
),由此利用公组求和法和裂项求和法能求出数列{bn}的前n项和Sn.
(Ⅱ)bn=(
| 2 |
| 4 |
| a2n-1a2n+1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
解答:
解:(Ⅰ)设f(x)=ax2+bx,
由其导函数f′(x)=2ax+b=2x-5,得a=1,b=-5,
∴f(x)=x2-5x,
当x∈(n+2,n+3),n∈n*时,
an=f(n+3)-f(n+2)=2n.
(Ⅱ)bn=(
)an+
(n∈N*)
=2n+
(
-
),
∴Sn=2+22+23+…+2n+
(1-
+
-
+…+
-
)
=
+
(1-
)
=2n+1-
.
由其导函数f′(x)=2ax+b=2x-5,得a=1,b=-5,
∴f(x)=x2-5x,
当x∈(n+2,n+3),n∈n*时,
an=f(n+3)-f(n+2)=2n.
(Ⅱ)bn=(
| 2 |
| 4 |
| a2n-1a2n+1 |
=2n+
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Sn=2+22+23+…+2n+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 2(1-2n) |
| 1-2 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
=2n+1-
| 3n+2 |
| 2n+1 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意分组求和法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
△ABC中,a=10,b=14,c=16,则△ABC中的最大角与最小角之和为( )
| A、90° | B、120° |
| C、135° | D、150° |
 函数f(x)=6cos2
函数f(x)=6cos2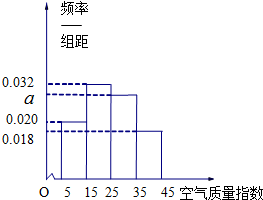 去年2月29日,我国发布了新修订的《环境空气质量标准》指出空气质量指数在0-50为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.
去年2月29日,我国发布了新修订的《环境空气质量标准》指出空气质量指数在0-50为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.