题目内容
 已知 如图,四边形ABCD是等腰梯形,AB∥DC,A(-1,-2),B(6,5),D(0,2).
已知 如图,四边形ABCD是等腰梯形,AB∥DC,A(-1,-2),B(6,5),D(0,2).(Ⅰ)求点C的坐标.
(Ⅱ)求等腰梯形ABCD对角线交点M的坐标.
考点:平面向量的坐标运算,两条直线的交点坐标
专题:平面向量及应用
分析:(I)利用向量共线定理和模的计算公式即可得出;
(II)分别求出直线AC与BD的方程即可得出.
(II)分别求出直线AC与BD的方程即可得出.
解答:
 解(Ⅰ)设C(x,y).
解(Ⅰ)设C(x,y).
∵A(-1,-2),B(6,5),D(0,2),
∴
=(x,y-2),
=(7,7),|
|2=(0+1)2+(2+2)2=17,
由已知,AB∥DC,|
|2=|
|2,
∴
,解得
或
.
当x=7,y=9时,四边形ABCD是平行四边形,舍去.
∴x=2,y=4,即C(2,4).
(Ⅱ)由(Ⅰ)知,直线AC的方程是
=
,即y=2x,
直线BD的方程是y=
x+2.
解方程组
,得
,
∴M(
,
).
 解(Ⅰ)设C(x,y).
解(Ⅰ)设C(x,y).∵A(-1,-2),B(6,5),D(0,2),
∴
| DC |
| AB |
| AD |
由已知,AB∥DC,|
| AD |
| CB |
∴
|
|
|
当x=7,y=9时,四边形ABCD是平行四边形,舍去.
∴x=2,y=4,即C(2,4).
(Ⅱ)由(Ⅰ)知,直线AC的方程是
| y+2 |
| 4+2 |
| x+1 |
| 2+1 |
直线BD的方程是y=
| 1 |
| 2 |
解方程组
|
|
∴M(
| 4 |
| 3 |
| 8 |
| 3 |
点评:本题考查了向量共线定理和模的计算公式、直线的方程与交点坐标,属于基础题.

练习册系列答案
相关题目
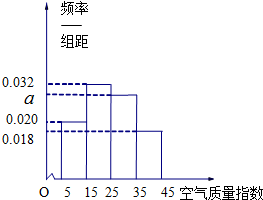 去年2月29日,我国发布了新修订的《环境空气质量标准》指出空气质量指数在0-50为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.
去年2月29日,我国发布了新修订的《环境空气质量标准》指出空气质量指数在0-50为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.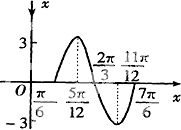 已知函数y=Asin(ωx+φ)(|φ|<
已知函数y=Asin(ωx+φ)(|φ|<