题目内容
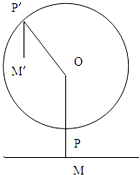 六一儿重节到了,小明与爸爸去游乐场看见了大观览车,已知大观览车轮轴中心为点O,距地面高为32m(即OM=32m),巨轮半径为30m,点p为吊舱与轮的连接点,吊舱高2m(即PM=2m)巨轮每分钟转动30°,小明和爸爸从地面M点进入吊舱后,巨轮开始逆时针转动.
六一儿重节到了,小明与爸爸去游乐场看见了大观览车,已知大观览车轮轴中心为点O,距地面高为32m(即OM=32m),巨轮半径为30m,点p为吊舱与轮的连接点,吊舱高2m(即PM=2m)巨轮每分钟转动30°,小明和爸爸从地面M点进入吊舱后,巨轮开始逆时针转动.(1)求4分钟后吊舱底部到地面的距离.
(2)设大观览车从小明和爸爸进入吊舱后经过t分钟到达P′M′处,求吊舱底部M′到地面的距离h与时间t(分钟)的函数关系式;
(3)用五点法作图画出当t∈[0,12]内的函数图象.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,五点法作函数y=Asin(ωx+φ)的图象
专题:三角函数的图像与性质
分析:(1)由题意求得PA=15(米),则4分钟后吊舱底部到地面的距离即可求出
(2)依题意,可设h=Asin(ωt+φ)+b,易求A=30,ω=
,b=30,由于h(0)=2,求得解析式.
(3)列表,描点连线即可.
(2)依题意,可设h=Asin(ωt+φ)+b,易求A=30,ω=
| π |
| 6 |
(3)列表,描点连线即可.
解答:
解:(1)巨轮每分钟转动30°
∴经过4分钟后,旋转了4×30°=120°;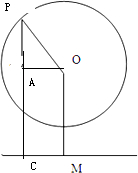
如图,连接OC,在⊙O上取P点,使∠MOP=120°,
分别过P,O作PC⊥CM于C,作OA⊥PC于A,
∵OP=30,
∴∠POM=120°-∠AOM=30°,
∴PA=15(米),
则:PC=15+30=45(米),
故分钟后吊舱底部到地面的距离45米.
(2)设大观览车转动时距离地面的高度h与时间t之间的函数关系式为:h=Asin(ωt+φ)+b,
∵每分钟转动30°,
∴大观览车逆时针旋转且每12分钟转动一圈,
∴T=
=12,解得ω=
,
又大观览车的半径为30m,即A=30,又观览车的轮轴的中心距地面32m,PM=2m,
∴b=32-2=30,
∴h=30sin(
t+φ)+30,
又当t=0时,h=2,
解得φ=-
∴h=30sin(
t-
)+30=30-30cos(
t),t∈(0,+∞)
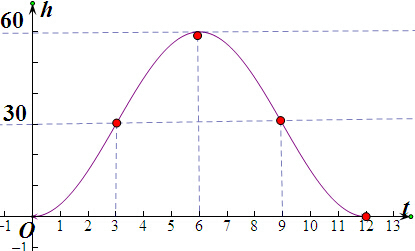
(3)列表
描点、连线如图所示.
∴经过4分钟后,旋转了4×30°=120°;

如图,连接OC,在⊙O上取P点,使∠MOP=120°,
分别过P,O作PC⊥CM于C,作OA⊥PC于A,
∵OP=30,
∴∠POM=120°-∠AOM=30°,
∴PA=15(米),
则:PC=15+30=45(米),
故分钟后吊舱底部到地面的距离45米.
(2)设大观览车转动时距离地面的高度h与时间t之间的函数关系式为:h=Asin(ωt+φ)+b,
∵每分钟转动30°,
∴大观览车逆时针旋转且每12分钟转动一圈,
∴T=
| 2π |
| ω |
| π |
| 6 |
又大观览车的半径为30m,即A=30,又观览车的轮轴的中心距地面32m,PM=2m,
∴b=32-2=30,
∴h=30sin(
| π |
| 6 |
又当t=0时,h=2,
解得φ=-
| π |
| 2 |
∴h=30sin(
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
(3)列表
描点、连线如图所示.
| t | 0 | 3 | 6 | 9 | 12 | ||||||
| 0 |
| π |
| 2π | ||||||
| h | 0 | 30 | 60 | 30 | 0 |

点评:本题考查函数y=Asin(ωx+φ)解析式的确定以及五点作图法,属于中档题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目