题目内容
1.甲、乙、丙三位同学上课后独立完成一份自我检测题,甲优秀的概率为$\frac{4}{5}$,乙优秀的概率为$\frac{2}{5}$,丙优秀的概率为$\frac{2}{3}$,则三人中至少有两人优秀的概率为( )| A. | $\frac{1}{25}$ | B. | $\frac{16}{25}$ | C. | $\frac{24}{25}$ | D. | $\frac{52}{75}$ |
分析 设甲优秀为事件A,乙优秀为事件B,丙优秀为事件C,则三人中至少有两人优秀的概率P=P(AB$\overline{C}$)+P(A$\overline{B}$C)+P($\overline{A}$BC)+P(ABC),由此能求出三人中至少有两人优秀的概率
解答 解:设甲优秀为事件A,乙优秀为事件B,丙优秀为事件C,
则三人中至少有两人优秀的概率P=P(AB$\overline{C}$)+P(A$\overline{B}$C)+P($\overline{A}$BC)+P(ABC),
=$\frac{4}{5}×\frac{2}{5}$×(1-$\frac{2}{3}$)+$\frac{4}{5}$×(1-$\frac{2}{5}$)×$\frac{2}{3}$+(1-$\frac{4}{5}$)×$\frac{2}{5}$×$\frac{2}{3}$+$\frac{4}{5}$×$\frac{2}{5}$×$\frac{2}{3}$=$\frac{8}{75}$+$\frac{24}{75}$+$\frac{4}{75}$+$\frac{16}{75}$=$\frac{12}{75}$,
故选:D
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意互斥事件概率加法公式和相互独立事件概率乘法公式、对立事件概率计算公式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.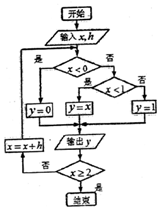 如果执行如图的程序框图,输入x=-2,h=2.5,那么输出的各个数的和等于( )
如果执行如图的程序框图,输入x=-2,h=2.5,那么输出的各个数的和等于( )
 如果执行如图的程序框图,输入x=-2,h=2.5,那么输出的各个数的和等于( )
如果执行如图的程序框图,输入x=-2,h=2.5,那么输出的各个数的和等于( )| A. | 1 | B. | 1.5 | C. | 2.5 | D. | 3 |
16.设变量x,y满足不等式$\left\{\begin{array}{l}{x+y≥3}\\{x-y≥-1}\\{2x-y≤3}\end{array}\right.$,则x2+y2的最小值是( )
| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{9}{2}$ | C. | $\sqrt{5}$ | D. | 2$\sqrt{5}$ |
5.已知z=$\frac{(1-i)^{2}}{1+i}$,则z的共轭复数的虚部为( )
| A. | i | B. | -i | C. | 1 | D. | -1 |