题目内容
9．
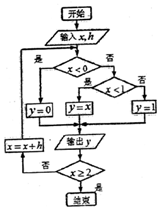如果执行如图的程序框图，输入x=-2，h=2.5，那么输出的各个数的和等于（ ）| A． | 1 | B． | 1.5 | C． | 2.5 | D． | 3 |
分析 结合框图，写出前几次循环得到结果，直到x的值大于等于2，退出循环，将各步的y值加起来即为输出的各个数的和．
解答 解：输入x=-2，h=2.5，
第1步：判断x=-2＜0成立，执行y=0，输出y，判断-2≥2不成立，执行x=-2+2.5=0.5；
第2步：判断x=0.5＜0不成立，再判断0.5＜1成立，执行y=0.5，输出y，判断0.5≥2不成立，执行x=0.5+2.5=3；
第3步：判断x=3＜0不成立，再判断3＜1不成立，执行y=1，输出y，判断3≥2成立，算法结束，退出循环．
输出各数和为：0+0.5+1=1.5．
故选：B．
点评 本题考查解决程序框图中的循环结构时，常采用写出前几次循环得到的结果，从中找到规律，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
17．已知菱形ABCD的边长为2，∠BAD=120°，点E，F分别在边BC，DC上，BE=EC，DF=λDC，若$\overrightarrow{AE}$•$\overrightarrow{AF}$=1，则λ的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{5}$ | D． | $\frac{1}{6}$ |
14．已知集合A={x∈N|（x+1）（2-x）≥0}，B{y|y=2x，x∈R}，则A∩B=（ ）
| A． | {x|0＜x≤2} | B． | {0，1，2} | C． | {1，2} | D． | {1} |
1．甲、乙、丙三位同学上课后独立完成一份自我检测题，甲优秀的概率为$\frac{4}{5}$，乙优秀的概率为$\frac{2}{5}$，丙优秀的概率为$\frac{2}{3}$，则三人中至少有两人优秀的概率为（ ）
| A． | $\frac{1}{25}$ | B． | $\frac{16}{25}$ | C． | $\frac{24}{25}$ | D． | $\frac{52}{75}$ |
13．设M、N分别是直线11：kx+y-k-4=0与直线l2：x-ky+2=0所过的两个定点，Q为线段MN的中点，P为直线11与直线l2的交点，则|PQ|=（ ）
| A． | $\frac{5}{2}$ | B． | 2 | C． | $\frac{3}{2}$ | D． | 1 |