题目内容
在复平面内，复数
（i是虚数单位）所对应的点位于（ ）
| 2+i |
| 4-3i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：根据复数的几何意义，即可得到结论．
解答：
解：z=
=
=
=
=
+
i，对应的点的坐标为（
，
）位于第一象限，
故选：A
| 2+i |
| 4-3i |
| (2+i)(4+3i) |
| (4-3i)(4+3i) |
| 8-3+10i |
| 16+9 |
| 5+10i |
| 25 |
| 1 |
| 5 |
| 2 |
| 5 |
| 1 |
| 5 |
| 2 |
| 5 |
故选：A
点评：本题主要考查复数的几何意义，利用复数的基本运算求解即可，比较基础．
练习册系列答案
相关题目
已知2a+b=t（a＞0，b＞0），t为常数，若ab的最大值为2时，a2+b2=（ ）
| A、2 | B、3 | C、4 | D、5 |
若tanα=1，则
的值为（ ）
| 2sinα+cosα |
| sinα-2cosα |
| A、1 | B、3 | C、-1 | D、-3 |
在各项均为正数的等比数列{an}中，a1=2，a2+a3=12．则该数列的前4项和为（ ）
| A、30 | B、32 | C、36 | D、40 |
某几何体的三视图如图所示，则该几何体外接球的表面积为（ ）
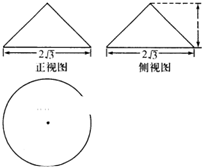
A、
| ||
B、
| ||
| C、4π | ||
| D、16π |
某科室派出4名调研员到3个学校，调研高三复习备考近况，要求每个学校至少一名，则不同的分配方案的种数是（ ）
| A、144 | B、72 | C、36 | D、48 |
已知角α的终边经过点P（m，4），且cosα=-
，则m等于（ ）
| 3 |
| 5 |
A、-
| ||
| B、-3 | ||
C、
| ||
| D、3 |
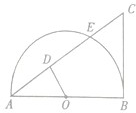如图，过点C作半圆O的切线CB，切点为B，直线AC与半圆O的交点分别为A、E，过圆心O作OD⊥AC垂点为D．