题目内容
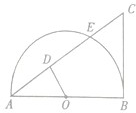 如图,过点C作半圆O的切线CB,切点为B,直线AC与半圆O的交点分别为A、E,过圆心O作OD⊥AC垂点为D.
如图,过点C作半圆O的切线CB,切点为B,直线AC与半圆O的交点分别为A、E,过圆心O作OD⊥AC垂点为D.(Ⅰ)若∠C=60°,CE=1,求BC的长;
(Ⅱ)求证OD•BC=OA•CE.
考点:与圆有关的比例线段
专题:选作题,立体几何
分析:(Ⅰ)连接BE,则∠AEB=90°,利用∠C=60°,CE=1,可求BC的长;
(Ⅱ)证明△AOD∽△BCE,即可证明OD•BC=OA•CE.
(Ⅱ)证明△AOD∽△BCE,即可证明OD•BC=OA•CE.
解答:
 (Ⅰ)解:连接BE,则∠AEB=90°,
(Ⅰ)解:连接BE,则∠AEB=90°,
∵∠C=60°,
∴BC=2CE=2;
(Ⅱ)证明:∵CB是半圆O的切线,
∴∠CBE=∠A,
∵∠CEB=∠ODA=90°,
∴△AOD∽△BCE,
∴
=
,
∴OD•BC=OA•CE.
 (Ⅰ)解:连接BE,则∠AEB=90°,
(Ⅰ)解:连接BE,则∠AEB=90°,∵∠C=60°,
∴BC=2CE=2;
(Ⅱ)证明:∵CB是半圆O的切线,
∴∠CBE=∠A,
∵∠CEB=∠ODA=90°,
∴△AOD∽△BCE,
∴
| OD |
| CE |
| AO |
| BC |
∴OD•BC=OA•CE.
点评:本题考查直径所对的圆周角为直角,考查三角形相似的判断与应用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
在复平面内,复数
(i是虚数单位)所对应的点位于( )
| 2+i |
| 4-3i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知函数f(x)=
x2+(a-1)x+3在区间(-∞,4]上单调递减,则a的取值范围( )
| 1 |
| 2 |
| A、[-3,+∞) |
| B、(-3,+∞) |
| C、(-∞,-3) |
| D、(-∞,-3] |
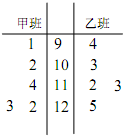 为了解甲、乙两个班级某次考试的数学成绩(单位:分),从甲、乙两个班级中分别随机抽取5名学生的成绩作样本,如图是样本的茎叶图.规定:成绩不低于120分时为优秀成绩.
为了解甲、乙两个班级某次考试的数学成绩(单位:分),从甲、乙两个班级中分别随机抽取5名学生的成绩作样本,如图是样本的茎叶图.规定:成绩不低于120分时为优秀成绩.