题目内容
14．有6名学生，其中有3名会唱歌，2名会跳舞，1名既会唱歌又会跳舞，现从中选出2名会唱歌的，1名会跳舞的，去参加文艺演出，求所有不同的选法种数为（ ）| A． | 18 | B． | 15 | C． | 16 | D． | 25 |
分析 4名会唱歌的从中选出两个有C42，3名会跳舞的选出1名有3种选法，其中一名既会唱歌又会跳舞的有一个，两组不能同时用他，减去同时用他的结果数．
解答 解：4名会唱歌的从中选出两个有C42=6种，
3名会跳舞的选出1名有3种选法，
但其中一名既会唱歌又会跳舞的有一个，
两组不能同时用他，
∴共有3×6-3=15种，
故选：B．
点评 按元素的性质分类是处理带限制条件的组合问题的常用方法，本题需要按照学生中的三种不同的情况来考虑问题．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
9．
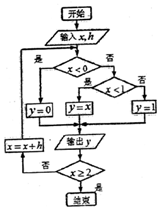如果执行如图的程序框图，输入x=-2，h=2.5，那么输出的各个数的和等于（ ）
如果执行如图的程序框图，输入x=-2，h=2.5，那么输出的各个数的和等于（ ）| A． | 1 | B． | 1.5 | C． | 2.5 | D． | 3 |
5．已知z=$\frac{（1-i）^{2}}{1+i}$，则z的共轭复数的虚部为（ ）
| A． | i | B． | -i | C． | 1 | D． | -1 |
9．不等式|2a-b|+|a+b|≥|a|（|x-1|+|x+1|）对于任意不为0的实数a，b恒成立，则实数x的范围为（ ）
| A． | $（-∞，-\frac{1}{2}]∪[\frac{1}{2}，+∞）$ | B． | $[-\frac{1}{2}，\frac{1}{2}]$ | C． | $（-∞，-\frac{3}{2}]∪[\frac{3}{2}，+∞）$ | D． | $[-\frac{3}{2}，\frac{3}{2}]$ |
19．某次数学考试的第一大题由10道四选一的选择题构成，要求考生从A，B，C，D中选出其中一项作为答案，每题选择正确得5分，选择错误不得分．以下是甲、乙、丙、丁四位考生的答案及甲、乙、丙三人的得分结果：
据此可以推算考生丁的得分是40．
| 题1 | 题2 | 题3 | 题4 | 题5 | 题6 | 题7 | 题8 | 题9 | 题10 | 得分 | |
| 甲 | C | B | D | D | A | C | D | C | A | D | 35 |
| 乙 | C | B | C | D | B | C | A | B | D | C | 35 |
| 丙 | C | A | D | D | A | D | A | B | A | C | 40 |
| 丁 | C | A | D | D | B | C | A | B | A | C | ？ |
3．已知函数$f（x）=\frac{1}{3}{x^3}-{x^2}+ax-5$在[-1，2]上不单调，则实数a的取值范围是（ ）
| A． | [-3，1） | B． | （-3，0） | C． | （-3，1） | D． | （-3，1] |
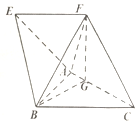如图，在四棱锥A-BCFE中，四边形EFCB为梯形，EF∥BC，且EF=$\frac{3}{4}$BC，△ABC是边长为2的正三角形，顶点F在AC上的射影为点G，且FG=$\sqrt{3}$，CF=$\frac{{\sqrt{21}}}{2}$，BF=$\frac{5}{2}$．