Question

4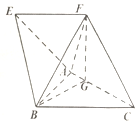．如图，在四棱锥A-BCFE中，四边形EFCB为梯形，EF∥BC，且EF=$\frac{3}{4}$BC，△ABC是边长为2的正三角形，顶点F在AC上的射影为点G，且FG=$\sqrt{3}$，CF=$\frac{{\sqrt{21}}}{2}$，BF=$\frac{5}{2}$．
（1）证明：平面FGB⊥平面ABC；
（2）求二面角E-AB-F的余弦值．

Answer 1

分析 （1）推导出FG⊥AC，取AC的中点为O，连结OB，GB，推导出FG⊥BG，FG⊥AC，从而FG⊥面ABC，由此能证明面FGB⊥面ABC．
（2）以OB所在直线为x轴，OC所在直线为y轴，过点O作平面ABC的垂线为z轴，建立空间直角坐标系，利用向量法能求出二面角E-AB-F的余弦值．

解答 证明：（1）由顶点F在AC上投影为点G，可知，FG⊥AC．
取AC的中点为O，连结OB，GB．
在Rt△FGC中，$FG=\sqrt{3}$，$CF=\frac{{\sqrt{21}}}{2}$，所以$CG=\frac{3}{2}$．
在Rt△GBO中，$OB=\sqrt{3}$，$OG=\frac{1}{2}$，所以$BG=\frac{{\sqrt{13}}}{2}$．
所以，BG²+GF²=FB²，即FG⊥BG．
∵FG⊥AC，FG⊥GB，AC∩BG=G
∴FG⊥面ABC．
又FG⊆面FGB，所以面FGB⊥面ABC．
解：（2）由（Ⅰ）知，OB⊥FG，OB⊥AC，且AC∩FG=G
所以  OB⊥面AFC，且FG⊥面ABC．以OB所在直线为x轴，OC所在直线为y轴，
过点O作平面ABC的垂线为z轴，建立空间直角坐标系，如图所示：
$A（0，-1，0），B（\sqrt{3}，0，0），F（0，-\frac{1}{2}，\sqrt{3}）$，E（$\frac{3\sqrt{3}}{4}$，-$\frac{5}{4}$，$\sqrt{3}$），
$\overrightarrow{BA}=（-\sqrt{3}，-1，0）$，$\overrightarrow{BE}$=（-$\frac{\sqrt{3}}{4}$，-$\frac{5}{4}$，$\sqrt{3}$），$\overrightarrow{BF}$=（-$\sqrt{3}，-\frac{1}{2}，\sqrt{3}$），
设平面ABE，ABF的法向量分别为$\overrightarrow{m}=（x，y，z）$，$\overrightarrow{n}=（a，b，c）$，
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{BA}=0}\\{\overrightarrow{m}•\overrightarrow{BE}=0}\end{array}\right.$，即$\left\{\begin{array}{l}{-\sqrt{3}x-y=0}\\{-\frac{\sqrt{3}}{4}x-\frac{5}{4}y+\sqrt{3}z=0}\end{array}\right.$，取x=1，得$\overrightarrow{m}$=（1，-$\sqrt{3}$，1），
$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{BA}=0\\ \overrightarrow n•\overrightarrow{BF}=0\end{array}\right.$，即$\left\{\begin{array}{l}{-\sqrt{3}a-b=0}\\{-\sqrt{3}a-\frac{1}{2}b+\sqrt{3}c=0}\end{array}\right.$，取a=1，得$\overrightarrow n=（1，-\sqrt{3}，\frac{1}{2}）$，
设二面角E-AB-F的平面角为θ．
则cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{\frac{9}{2}}{\sqrt{5}•\sqrt{\frac{17}{4}}}$=$\frac{9\sqrt{85}}{85}$．
所以二面角E-AB-F的余弦值为$\frac{9\sqrt{85}}{85}$．

点评 本题考查面面垂直的证明，考查二面角的余弦值的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想、数形结合思想，是中档题．