题目内容
设集合A={-2},B={x|ax+1=0,a∈R},若A∩B=B,则a的取值集合为 .
考点:交集及其运算
专题:集合
分析:求出集合A,将条件A∩B=B转化为B⊆A,即可求a的取值集合.
解答:
解:集合A={-2},
∵A∩B=B,
∴B⊆A,
若a=0,则B=∅,满足条件B⊆A,
若a≠0,则B={x|ax+1=0,x∈R}={x|x=-
},
要使B⊆A成立,
则-
=-2,
解得a=-
,
综上:a的取值集合为{0,
}.
故答案为:{0,
}.
∵A∩B=B,
∴B⊆A,
若a=0,则B=∅,满足条件B⊆A,
若a≠0,则B={x|ax+1=0,x∈R}={x|x=-
| 1 |
| a |
要使B⊆A成立,
则-
| 1 |
| a |
解得a=-
| 1 |
| 2 |
综上:a的取值集合为{0,
| 1 |
| 2 |
故答案为:{0,
| 1 |
| 2 |
点评:本题主要考查集合的基本运算以及集合关系的应用,注意对集合B要注意讨论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
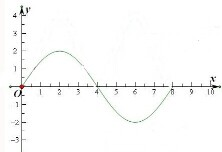 已知函数f(x)=Asinωx(A>0,ω<0)的部分图象如图所示,则函数f(x)是( )
已知函数f(x)=Asinωx(A>0,ω<0)的部分图象如图所示,则函数f(x)是( )| A、周期为8的偶函数 |
| B、周期为8的奇函数 |
| C、周期为8π的偶函数 |
| D、周期为8π的奇函数 |
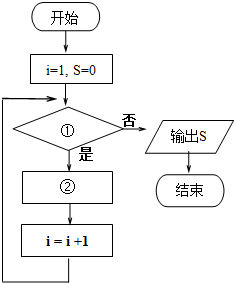 已知等比数列{an}中,a1=1,公比q=2,计算数列{an}的前20项的和S,现已给出该算法的程序框图如图所示:
已知等比数列{an}中,a1=1,公比q=2,计算数列{an}的前20项的和S,现已给出该算法的程序框图如图所示: