题目内容
关于x的方程x2+2(m+1)x+2m+6=0的两实根为α和β,根据下列条件求m的范围.
(1)α<2<β;
(2)α<1且β>3.
(1)α<2<β;
(2)α<1且β>3.
考点:一元二次方程的根的分布与系数的关系
专题:计算题,函数的性质及应用
分析:令f(x)=x2+2(m+1)x+2m+6,将方程的根化为函数图象与x轴的交点.
解答:
解:令f(x)=x2+2(m+1)x+2m+6,
(1)∵α<2<β,
∴f(2)=4+4(m+1)+2m+6<0,
解得,m<-
;
(3)∵α<1且β>3,
∴f(1)=1+2m+2+2m+6<0,
f(3)=9+2(m+1)3+2m+6<0,
解得,m<-
.
(1)∵α<2<β,
∴f(2)=4+4(m+1)+2m+6<0,
解得,m<-
| 7 |
| 3 |
(3)∵α<1且β>3,
∴f(1)=1+2m+2+2m+6<0,
f(3)=9+2(m+1)3+2m+6<0,
解得,m<-
| 21 |
| 8 |
点评:本题考查了方程的根与函数的零点之间的关系,借助图象解答,属于基础题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
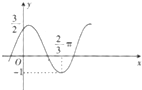 将函数y=Asinωx+b(A,ω,b均为正实数)的图象向左平移
将函数y=Asinωx+b(A,ω,b均为正实数)的图象向左平移| π |
| 12 |
A、y=2sin(x+
| ||||||
B、y=
| ||||||
C、y=
| ||||||
D、y=
|