题目内容
已知函数f(x)=x|x-a|,a∈R,解不等式f(x)≥2a2.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:将不等式去绝对值,化为两个不等式组,然后对a的符号讨论解之.
解答:
解:由题设知x|x-a|≥2a2,
∴原不等式等价于
①
或
②
由①得
解得x∈∅.
由②得
,
当a=0时,x≥0.
当a>0时,
,∴x≥2a.
当a<0时,
即x≥-a.
综上,a≥0时,f(x)≥2a2的解集为{x|x≥2a};
a<0时,f(x)≥2a2的解集为{x|x≥-a}.
∴原不等式等价于
|
或
|
由①得
|
由②得
|
当a=0时,x≥0.
当a>0时,
|
当a<0时,
|
即x≥-a.
综上,a≥0时,f(x)≥2a2的解集为{x|x≥2a};
a<0时,f(x)≥2a2的解集为{x|x≥-a}.
点评:主要考查了绝对值不等式解法以及讨论思想的运用.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
若函数f(x)=2-|x|-c的图象与x轴有公共点,则实数c的职值范围是( )
| A、[一1,0) |
| B、[0,1] |
| C、(0,1] |
| D、[1,+∞) |
 对某班学生一次英语测试的成绩分析,各分数段的分布如图(分数取整数),由此,估计这次测验的优秀率(不小于80分)为
对某班学生一次英语测试的成绩分析,各分数段的分布如图(分数取整数),由此,估计这次测验的优秀率(不小于80分)为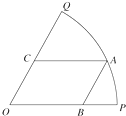 地震过后,当地人民积极恢复生产,焊工王师傅每天都很忙碌.今天他遇到了一个难题:如图所示,有一块扇形钢板,半径为1m,圆心角θ=
地震过后,当地人民积极恢复生产,焊工王师傅每天都很忙碌.今天他遇到了一个难题:如图所示,有一块扇形钢板,半径为1m,圆心角θ=