题目内容
方程
=kx+2有两个不同的实数根,则实数k的取值范围为 .
| 1-x2 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:将问题转化为两个函数的交点问题,画出函数图象,结合图象,从而求出k的范围.
解答:
解:解:设y=f(x)=
,(y≥0,0≤x≤1);即x2+y2=1 (半圆),
y=h(x)=kx+2 (x∈R) 即y-2=kx,直线恒过点M(0,2),
∵方程f(x)=h(x)有两个不同的实数根,(k>0)即y=f(x)和y=h(x)有两个不同的交点,
画出f(x),h(x)的图象,如图示:
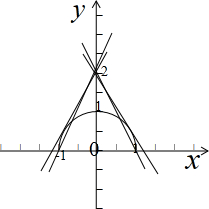 ,
,
当直线与圆相切时,k=±
,
当直线过(0,2),(-1,0)时,k=±2,
∴-2≤k<-
或
<k≤2,
故答案为:[-2,-
)∪(
,2].
| 1-x2 |
y=h(x)=kx+2 (x∈R) 即y-2=kx,直线恒过点M(0,2),
∵方程f(x)=h(x)有两个不同的实数根,(k>0)即y=f(x)和y=h(x)有两个不同的交点,
画出f(x),h(x)的图象,如图示:
 ,
,当直线与圆相切时,k=±
| 3 |
当直线过(0,2),(-1,0)时,k=±2,
∴-2≤k<-
| 3 |
| 3 |
故答案为:[-2,-
| 3 |
| 3 |
点评:本题考查了函数的零点问题,考查了转化思想,是一道中档题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
若圆(x-a)2+(y-b)2=c2和圆(x-b)2+(y-a)2=c2相切,则( )
| A、(a-b)2=c2 |
| B、(a-b)2=2c2 |
| C、(a+b)2=c2 |
| D、(a+b)2=2c2 |
已知双曲线E:
-
=1(a>0,b>0)的右焦点为F(3,0),过点F的直线交双曲线于A,B两点,若AB的中点坐标为N(-12,-15),则E的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
求适合下列条件的椭圆的标准方程:
(1)一条准线方程为y=
,离心率为
;
(2)与椭圆
+
=1有相同的焦点,且经过点(1,
);
(3)经过A(4,
),B(-3,-
)两点.
(1)一条准线方程为y=
| 9 |
| 2 |
| 2 |
| 3 |
(2)与椭圆
| x2 |
| 16 |
| y2 |
| 15 |
| 3 |
| 2 |
(3)经过A(4,
| 12 |
| 5 |
| 16 |
| 5 |
已知△ABC中c=4,a=4
,C=30°,则A等于( )
| 3 |
| A、60° |
| B、60°或120° |
| C、30° |
| D、30°或150° |
已知a<0,-1<b<0,那么( )
| A、a>ab>ab2 |
| B、ab2>ab>a |
| C、ab>a>ab2 |
| D、ab>ab2>a |
