题目内容
 如图,若正四棱柱ABCD-A1B1C1D1的底面边长为2,高为4,则异面直线BD1与AD所成角的正弦值是
如图,若正四棱柱ABCD-A1B1C1D1的底面边长为2,高为4,则异面直线BD1与AD所成角的正弦值是考点:异面直线及其所成的角
专题:空间位置关系与距离
分析:根据正四棱柱的几何特征,我们易根据AD∥BC,得到∠D1BC即为异面直线BD1与AD所成角,根据已知中正四棱柱ABCD-A1B1C1D1的底面边长为2,高为4,求出△D1BC中各边的长,解△D1BC即可得到答案.
解答:
解:∵AD∥BC
∴∠D1BC即为异面直线BD1与AD所成角,
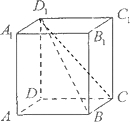
连接D1C,在△D1BC中,
∵正四棱柱ABCD-A1B1C1D1的底面边长为2,高为4,
∴D1B=2
,BC=2,D1C=2
∴sin∠D1BC=
=
=
,
故异面直线BD1与AD所成角的正弦值是
,
故答案为:
∴∠D1BC即为异面直线BD1与AD所成角,

连接D1C,在△D1BC中,
∵正四棱柱ABCD-A1B1C1D1的底面边长为2,高为4,
∴D1B=2
| 6 |
| 5 |
∴sin∠D1BC=
| D1C |
| D1B |
2
| ||
2
|
| ||
| 6 |
故异面直线BD1与AD所成角的正弦值是
| ||
| 6 |
故答案为:
| ||
| 6 |
点评:本题考查的知识点是异面直线及其所成的角,其中根据已知条件确定找到两条异面直线夹角是解答本题的关键.

练习册系列答案
相关题目
设a>0且a≠1,则“函数f(x)=ax在x上是减函数”,是“函数g(x)=(2-a)x3在R上是增函数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
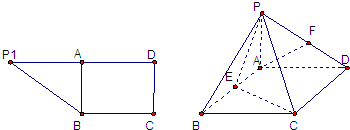
 如图,PA⊥平面ABC,∠ABC=90°且PA=AB=BC=a,则异面直线PB与AC所成角的正切值等于
如图,PA⊥平面ABC,∠ABC=90°且PA=AB=BC=a,则异面直线PB与AC所成角的正切值等于