题目内容
4．函数y=4x-2x+1，x∈[-3，2]的最大值为13．分析 令2x=t，由-3≤x≤2，可得$\frac{1}{8}$≤t≤4，y=t2-t+1，t∈[$\frac{1}{8}$，4]．再利用二次函数的性质求得y的最大值．
解答 解：y=（2x）2-2x+1，令2x=t，
∵-3≤x≤2，∴$\frac{1}{8}$≤2x≤4，
∴y=t2-t+1，t∈[$\frac{1}{8}$，4]．
由于函数 y=（t-$\frac{1}{2}$）2+$\frac{3}{4}$的对称轴为 t=$\frac{1}{2}$，
∴当t=4时，ymax=16-4+1=13，
故答案为：13．
点评 本题主要考查复合函数的单调性，二次函数的性质的应用，属于中档题．
练习册系列答案
相关题目
15．已知双曲线的焦距为2$\sqrt{3}$，焦点到一条渐近线的距离为$\sqrt{2}$，则双曲线的标准方程为（ ）
| A． | x2-$\frac{{y}^{2}}{2}$=1 | B． | $\frac{{x}^{2}}{2}$-y2=1 | ||
| C． | x2-$\frac{{y}^{2}}{2}$=1或y2-$\frac{{x}^{2}}{2}$=1 | D． | $\frac{{x}^{2}}{2}$-y2=1或$\frac{{y}^{2}}{2}$-x2=1 |
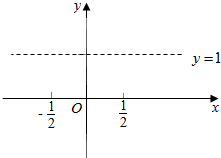已知直线y=1与曲线y=x2-|x|+a有四个交点．