已知直线y=1与曲线y=x2-|x|+a有四个交点．=x2-|x|+a为偶函数．的解析式.并作出符合已知条件的函数f(x)图象．(3)求a的取值范围．题目和参考答案——青夏教育精英家教网—

题目内容

12．

已知直线y=1与曲线y=x²-|x|+a有四个交点．
（1）求证：f（x）=x²-|x|+a为偶函数．
（2）求当x≥0时，f（x）的解析式，并作出符合已知条件的函数f（x）图象．
（3）求a的取值范围．

分析（1）根据偶函数的定义即可证明，
（2）根据x≥0，得到函数f（x）的解析式，
（3）在同一坐标系中，作出y=1，y=x²-|x|+a，由图可知a的取值范围．

解答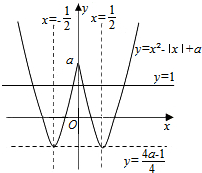解：（1）∵f（x）=x²-|x|+a的定义域为R，
∴f（-x）=（-x）²-|-x|+a=x²-|x|+a=f（x），
∴f（x）为偶函数；
（2）当x≥0时，f（x）=x²-x+a，图象如图所示：
（3）如图，在同一坐标系中，作出y=1，y=x²-|x|+a，由图可知a必须满足$\left\{\begin{array}{l}{a＞1}\\{\frac{4a-1}{4}＜1}\end{array}\right.$，解得1＜a＜$\frac{5}{4}$，
故a的取值范围为（1，$\frac{5}{4}$）．

点评本题考查了函数的图象的作法和函数图象的交点问题，属于中档题．

练习册系列答案

3．在平面直角坐标系中，已知函数y=log_a（x-3）+2（a＞0，且a≠1）过定点P，且角α的终边过点P，始边是以x正半轴为始边，则3sin²α+cos2α的值为$\frac{6}{5}$．

20．过双曲线$\frac{{x}^{2}}{3}$-y²=1的两焦点作实轴的垂线，分别与渐近线交于A、B、C、D四点，则矩形ABCD的面积为（　　）

A．

$\frac{16}{3}$$\sqrt{3}$

B．

C．

D．

7．函数f（x）=x²-2x-3在[0，3）上的值域为[-4，0）．

17．有四个命题
①p：f（x）=lnx-2+λ在区间（1，2）上有一个零点，q：e^0.2＞e^0.3，p∧q为真命题
②当x＞1时，f（x）=x²，g（x）=x${\;}^{\frac{1}{3}}$，h（x）=x^-2的大小关系是h（x）＜g（x）＜f（x）
③若f′（x₀）=0，则f（x）在x=x₀处取得极值
④若不等式2-3x-2x²＞0的解集为P，函数y=$\sqrt{x+2}$+$\sqrt{1-2x}$的定义域为Q，则“x∈P”是“x∈Q”的充分不必要条件，其中正确命题的个数是（　　）

4．函数y=4^x-2^x+1，x∈[-3，2]的最大值为13．

1．将函数$f（x）=2sin（{2x+\frac{π}{4}}）$的图象向左平移φ（φ＞0）个单位长度后图象关于直线$x=\frac{π}{2}$对称，则φ的最小值为$\frac{π}{8}$．

2．下列命题中的假命题是（　　）

	A．	?x∈R，x³＜0
	B．	在斜二测画法中，直观图的面积是原图形面积的4$\sqrt{2}$
	C．	“a＞0”是“\|a\|＞0”充分不必要的条件
	D．	关于x的不等式x²-2ax-8a²＜0（a＞0）的解集为（x₁，x₂），且x₂-x₁=15，则$a=\frac{5}{2}$

试题分类