题目内容

14．“函数f（x）在R上单调递减”是“f′（x）＜0在R上恒成立”的必要不充分条件．

分析 利用导函数的性质与函数增减性间的关系判断即可．

解答 解：若f′（x）＜0在R上恒成立，则有函数f（x）在R上单调递减；
反之，函数f（x）在R上单调递减，则有f′（x）≤0在R上恒成立，
则“函数f（x）在R上单调递减”是“f′（x）＜0在R上恒成立”的必要不充分条件，
故答案为：必要不充分

点评 此题考查了必要条件、充分条件与充要条件的判断，熟练掌握导函数的性质是解本题的关键．

练习册系列答案
相关题目
1．集合A={-1，0，1，3}，集合B={x|x2-x-2≤0，x∈N}，全集U={x||x-1|≤4，x∈Z}，则A∩（∁UB）=（　　）
A．{3}B．{-1，3}C．{-1，0，3}D．{-1，1，3}
5．已知数列$\{a_n^{\;}\}$满足a1=2，${a_{n+1}}=2{a_n}+2\;\;（n∈{N^*}）$．
（1）求数列$\{a_n^{\;}\}$的通项公式an；
（2）若数列$\{b_n^{\;}\}满足b_n^{\;}={log_2}（{a_n}+2）$，设Tn是数列$\{\frac{b_n}{{{a_n}+2}}\}$的前n项和，求证：${T_n}＜\frac{3}{2}$．
2．若tanα=3，则sin2α+2cos2α=$\frac{11}{10}$．
9．双曲线$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{12}=1$的实轴长为（　　）
A．2B．2$\sqrt{3}$C．4D．4$\sqrt{3}$
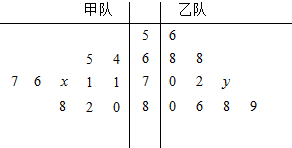19．下面的茎叶图记录了甲、乙两代表队各10名同学在一次数学竞赛中的成绩（单位：分），已知甲代表队数据的中位数为76，乙代表队数据的平均数是75．
（1）求x，y的值，并判断甲、乙两队谁的成绩更稳定？（不需要说明理由）
（2）若分别从甲、乙两队随机各抽取1名成绩不低于80分的学生，求抽到学生中，甲队学生成绩不低于乙队学生成绩的概率．
6．若函数y=f（x）的定义域是[-2，2]，则函数g（x）=$\frac{f（2x）}{x}$的定义域是[-1，0）∪（0，1]．
3．在平面直角坐标系中，已知函数y=loga（x-3）+2（a＞0，且a≠1）过定点P，且角α的终边过点P，始边是以x正半轴为始边，则3sin2α+cos2α的值为$\frac{6}{5}$．
4．函数y=4x-2x+1，x∈[-3，2]的最大值为13．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网