题目内容
在平面直角坐标系xOy中,已知点A(1,0),点B在直线l:x=-1上运动,过点B与直线l垂直的直线和线段AB的垂直平分线相交于点M.
(1)求动点M的轨迹E的方程;
(2)在x轴上是否存在点N,使过点N的直线与轨迹E恒有两个交点P、Q,且满足
•
=5?若存在,求出点N的坐标;若不存在,请说明理由.
(1)求动点M的轨迹E的方程;
(2)在x轴上是否存在点N,使过点N的直线与轨迹E恒有两个交点P、Q,且满足
| OP |
| OQ |
考点:轨迹方程
专题:综合题
分析:(1)由过点B与直线l垂直的直线和线段AB的垂直平分线相交于点M,可知,MA=MB,所以点M的轨迹是以A(1,0)为焦点的抛物线;(2)先假设存在N(a,0),过P,Q的直线方程为x=my+a,再结合
•
=5可求.
| OP |
| OQ |
解答:
解:(1)由题意,点M的轨迹是以A(1,0)为焦点的抛物线,设方程为y2=2px(p>0),则
=1,∴动点M的轨迹E的方程是y2=4x;
(2)设存在N(a,0),过P,Q的直线方程为x=my+a,代入y2=4x,得 y2-4my-4a=0,设P(
, y1),Q(
,y2),则y1y2=4a,又
•
=5,得a2+4a-5=0,解得a=1或a=-5.
经检验a=-5不满足过点N的直线与轨迹E恒有两个交点P、Q,故舍去
故a=1
| p |
| 2 |
(2)设存在N(a,0),过P,Q的直线方程为x=my+a,代入y2=4x,得 y2-4my-4a=0,设P(
| ||
| 2p |
| ||
| 2p |
| OP |
| OQ |
经检验a=-5不满足过点N的直线与轨迹E恒有两个交点P、Q,故舍去
故a=1
点评:本题主要考查抛物线的定义,及存在性问题的探求,存在性问题通常假设存在,从而转化为封闭型问题解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
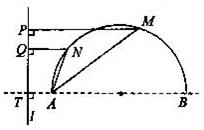 如图,已知半圆的直径|AB|=20,l为半圆外一直线,且与BA的延长线交于点T,|AT|=4,半圆上相异两点M、N与直线l的距离|MP|、|NQ|满足条件
如图,已知半圆的直径|AB|=20,l为半圆外一直线,且与BA的延长线交于点T,|AT|=4,半圆上相异两点M、N与直线l的距离|MP|、|NQ|满足条件| |MP| |
| |MA| |
| |NQ| |
| |NA| |
| A、22 | B、20 | C、18 | D、16 |
若
=b,则a+b=( )
| lim |
| x→1 |
| x+a | |||
|
| A、-2 | B、0 | C、2 | D、4 |
直线l与平面a内的两条直线都垂直,则直线l与平面a的位置关系是( )
| A、平行 | B、垂直 |
| C、在平面a内 | D、无法确定 |
