题目内容
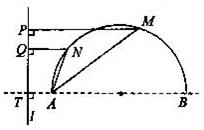如图，已知半圆的直径|AB|=20，l为半圆外一直线，且与BA的延长线交于点T，|AT|=4，半圆上相异两点M、N与直线l的距离|MP|、|NQ|满足条件| |MP| |
| |MA| |
| |NQ| |
| |NA| |
| A、22 | B、20 | C、18 | D、16 |
考点：圆与圆锥曲线的综合,抛物线的定义
专题：计算题,压轴题
分析：先以AT的中点O为坐标原点，AT的中垂线为y轴，可得半圆方程为（x-12）2+y2=100，根据条件得出M，N在以A为焦点，PT为准线的抛物线上，联立半圆方程和抛物线方程结合根与系数的关系，利用抛物线的定义即可求得答案．
解答：
解：以AT的中点O为坐标原点，AT的中垂线为y轴，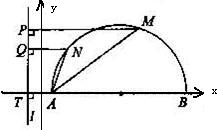
可得半圆方程为（x-12）2+y2=100
又
=
=1，设M（x1，y1），N（x2，y2），
M，N在以A为焦点，PT为准线的抛物线上；
以AT的垂直平分线为y轴，TA方向为x轴建立坐标系，
则有
物线方程为y2=8x（y≥0），联立半圆方程和抛物线方程，
消去y得：x2-16x+44=0
∴x1+x2=16，
|AM|+|AN|=|MP|+|NQ|=x1+x2+4=20．
故选：B．
可得半圆方程为（x-12）2+y2=100
又
| |MP| |
| |MA| |
| |NQ| |
| |NA| |
M，N在以A为焦点，PT为准线的抛物线上；
以AT的垂直平分线为y轴，TA方向为x轴建立坐标系，
则有
物线方程为y2=8x（y≥0），联立半圆方程和抛物线方程，
消去y得：x2-16x+44=0
∴x1+x2=16，
|AM|+|AN|=|MP|+|NQ|=x1+x2+4=20．
故选：B．
点评：本小题主要考查抛物线的定义、圆的方程、圆与圆锥曲线的综合等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于基础题．
练习册系列答案
相关题目
圆锥的侧面面积是底面面积的2倍，则圆锥的母线与底面所成的角为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知直线z的极坐标方程为ρcos(θ-
) =
，点A的极坐标为（4，
），则点A到直线l的距离为（ ）
| 3π |
| 4 |
| 2 |
| π |
| 4 |
A、
| ||||
| B、1 | ||||
C、
| ||||
| D、2 |
设图中的正方体的棱长为a（1）图中哪些棱所在的直线与直线BA1成异面直线？（2）求直线BA1和CC1所成的角的大小．（3）求异面直线BC和AA1的距离．