题目内容
假设电梯在每层停的概率相等且相互独立,则十层电梯从低层到顶层停不少于3次的概率是多少?停几次概率最大?数学期望是多少?
考点:n次独立重复试验中恰好发生k次的概率,离散型随机变量及其分布列,离散型随机变量的期望与方差
专题:计算题
分析:由于电梯在每层停的概率相等且相互独立,十层电梯从低层到顶层停不少于3次,包括停3次,停4次,停5次,…直到停9次,根据相互独立事件概率加法公式,我们计算出停3次,停4次,…,停9次的概率,进而即可得到答案.设从低层到顶层停k次,我们易计算其概率,根据组合数公式,易分析出结论,又由各层停的概率均为
,根据二项分布公式,易得到其数学期望.
| 1 |
| 2 |
解答:
解:依题意,从低层到顶层停不少于3次,应包括停3次,停4次,停5次,…直到停9次(2分)
∴从低层到顶层停不少于3次的概率
P=
(
)3(
)6+
(
)4(
)5+
(
)5(
)4+…+
(
)9 =
+
+
+…+
)(
)9=
(6分)
设从低层到顶层停k次,则其概率为
(
)k(
)9-k=
(
)9 ,
∴当k=4或k=5时,C9k最大,即
(
)9 最大.(9分)
其分布为二项分布,所以E(ξ)=9•
=
答:从低层到顶层停不少于3次的概率为
,停4次或5次概率最大,其数学期望为
(13分)
∴从低层到顶层停不少于3次的概率
P=
| C | 3 9 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 4 9 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 5 9 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 9 9 |
| 1 |
| 2 |
| (C | 3 9 |
| C | 4 9 |
| C | 5 9 |
| C | 9 9 |
| 1 |
| 2 |
| 233 |
| 256 |
设从低层到顶层停k次,则其概率为
| C | k 9 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | k 9 |
| 1 |
| 2 |
∴当k=4或k=5时,C9k最大,即
| C | k 9 |
| 1 |
| 2 |
其分布为二项分布,所以E(ξ)=9•
| 1 |
| 2 |
| 9 |
| 2 |
答:从低层到顶层停不少于3次的概率为
| 233 |
| 256 |
| 9 |
| 2 |
点评:本题考查的知识点是n次独立重复试验中恰好发生k次的概率,离散型随机变量及其分布列,离散型随机变量的期望,要想计算一个事件的概率,首先我们要分析这个事件是分类的(分几类)还是分步的(分几步),然后再利用加法原理和乘法原理进行求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设ξ的概率密度函数为f(x)=
e-
,则下列结论错误的是( )
| 1 | ||
|
| (x-1)2 |
| 2 |
| A、p(ξ<1)=p(ξ>1) |
| B、p(-1≤ξ≤1)=p(-1<ξ<1) |
| C、f(x)的渐近线是x=0 |
| D、η=ξ-1~N(0,1) |
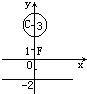 如图,已知F(0,1),直线l:y=-2,圆C:x2+(y-3)2=1
如图,已知F(0,1),直线l:y=-2,圆C:x2+(y-3)2=1