题目内容
已知函数f(x)=
(x-a)2+lnx(a为常数).
(1)若函数在x=1处的切线斜率为2,求该切线的方程;
(2)当x∈(1,3)时,f(x)>x+
a2-a-
恒成立,求a的取值范围.
| 1 |
| 2 |
(1)若函数在x=1处的切线斜率为2,求该切线的方程;
(2)当x∈(1,3)时,f(x)>x+
| 1 |
| 2 |
| 1 |
| 2 |
考点:函数恒成立问题,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)若函数在x=1处的切线斜率为2,求该切线的方程;
(2)构造函数,求函数的导数,利用导数和最值之间的关系即可得到结论.
(2)构造函数,求函数的导数,利用导数和最值之间的关系即可得到结论.
解答:
解:(1)函数的定义域为(0,+∞),则函数的导数f′(x)=x-a+
,
若函数在x=1处的切线斜率为2,
则f′(1)=2,即1-a+1=2,即a=0,
又f(1)=
,
则该切线的方程为y-
=2(x-1),
即4x-2y-3=0;
(2)令g(x)=f(x)-x-(
a2-a-
)=
x2+lnx-(a+1)x+a+
,
则g(1)=0,g′(x)=x+
-(a+1),
令h(x)=x+
-(a+1),
则当x∈(1,3)时,h(x)为增函数,值域为(2,
),
①当a+1≤2,即a≤1,g′(x)>0,函数g(x)在(1,3)上为增函数,则g(x)>g(1)=0,∴a≤1成立.
②a+1≥
,即a≥
,g′(x)<0,则函数g(x)在(1,3)上为减函数,则g(x)<g(1)=0,
此时不满足条件.
③2<a+1<
,即1<a<
时,g′(x)=0,有两个根x1,x2,
其中x1=
<1,x2=
>1,
∴g′(x)=
=
当1<x<x2时,g′(x)<0,则函数g(x)在(1,x2)上为减函数,则g(x)<g(1)=0,不符号题意,
此时不成立,
综上a的取值范围为(-∞,1].
| 1 |
| x |
若函数在x=1处的切线斜率为2,
则f′(1)=2,即1-a+1=2,即a=0,
又f(1)=
| 1 |
| 2 |
则该切线的方程为y-
| 1 |
| 2 |
即4x-2y-3=0;
(2)令g(x)=f(x)-x-(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则g(1)=0,g′(x)=x+
| 1 |
| x |
令h(x)=x+
| 1 |
| x |
则当x∈(1,3)时,h(x)为增函数,值域为(2,
| 10 |
| 3 |
①当a+1≤2,即a≤1,g′(x)>0,函数g(x)在(1,3)上为增函数,则g(x)>g(1)=0,∴a≤1成立.
②a+1≥
| 10 |
| 3 |
| 7 |
| 3 |
此时不满足条件.
③2<a+1<
| 10 |
| 3 |
| 7 |
| 3 |
其中x1=
a+1-
| ||
| 2 |
a+1+
| ||
| 2 |
∴g′(x)=
| x2-(a+1)x+1 |
| x |
| (x-x1)(x-x2) |
| x |
当1<x<x2时,g′(x)<0,则函数g(x)在(1,x2)上为减函数,则g(x)<g(1)=0,不符号题意,
此时不成立,
综上a的取值范围为(-∞,1].
点评:本题主要考查导数的几何意义以及利用导数求函数的最值,综合性较强,运算量较大.

练习册系列答案
相关题目
已知函数f(x)=
,则下列结论正确的是( )
|
| A、f(x)是偶函数 |
| B、f(x)是增函数 |
| C、f(x)是周期函数 |
| D、f(x)的值域为[0,+∞) |
现要完成下列3项抽样调查:
①从10盒酸奶中抽取3盒进行食品卫生检查;
②科技报告厅有32排作为,每排40个座位,有一次报告会恰好坐满了听众,报告会结束后,为了听取意见,邀请32名听众进行座谈;
③某中学高三年级有12个班,文科班4个,理科班8个,为了了解全校学生对知识的掌握情况,拟抽取一个容量为50的样本.
较为合理的抽样方法是( )
①从10盒酸奶中抽取3盒进行食品卫生检查;
②科技报告厅有32排作为,每排40个座位,有一次报告会恰好坐满了听众,报告会结束后,为了听取意见,邀请32名听众进行座谈;
③某中学高三年级有12个班,文科班4个,理科班8个,为了了解全校学生对知识的掌握情况,拟抽取一个容量为50的样本.
较为合理的抽样方法是( )
| A、①简单随机抽样,②系统抽样,③分层抽样 |
| B、①简单随机抽样,②分层抽样,③系统抽样 |
| C、①系统抽样,②简单随机抽样,③分层抽样 |
| D、①分层抽样,②系统抽样,③简单随机抽样 |
△ABC中,下面四个等式中不正确的是( )
| A、cos(A+B)=-cosC | ||||
| B、sin2(A+B)=sin2C | ||||
C、tan
| ||||
D、cos3(A+B)=1-2cos2
|
若不等式组
表示的平面区域是一个三角形,则a的取值范围是( )
|
| A、[0,3] |
| B、[0,3) |
| C、[3,6) |
| D、[3,6] |
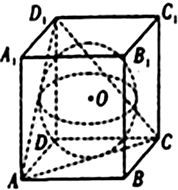 如图,已知球O是棱长为1的正方体ABCD-A1B1C1D1的内切球,则以B1为顶点,以球被平面ACD1截得的圆为底面的圆锥的全面积为
如图,已知球O是棱长为1的正方体ABCD-A1B1C1D1的内切球,则以B1为顶点,以球被平面ACD1截得的圆为底面的圆锥的全面积为