题目内容
若sinα=
,cos(α+β)=-
,且α,β是锐角,则β等于( )
4
| ||
| 7 |
| 11 |
| 14 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:两角和与差的余弦函数
专题:三角函数的求值
分析:根据角的范围和平方关系求出sin (α+β)、cosα的值,再由cos β=cos[(α+β)-α]和两角差的余弦公式求值,再求出角α的值即可.
解答:
解:由题意知,α,β是锐角,则0°<α+β<180°,
又sinα=
,cos(α+β)=-
,
所以sin (α+β)=
=
=
,
cosα=
=
,
所以cos β=cos[(α+β)-α]=cos(α+β)cosα+sin (α+β)sinα
=(-
)×
+
×
=
,
又β是锐角,则β=
,
故选:A.
又sinα=
4
| ||
| 7 |
| 11 |
| 14 |
所以sin (α+β)=
| 1-cos2(α+β) |
1-
|
5
| ||
| 14 |
cosα=
| 1-sin2α |
| 1 |
| 7 |
所以cos β=cos[(α+β)-α]=cos(α+β)cosα+sin (α+β)sinα
=(-
| 11 |
| 14 |
| 1 |
| 7 |
5
| ||
| 14 |
4
| ||
| 7 |
| 1 |
| 2 |
又β是锐角,则β=
| π |
| 3 |
故选:A.
点评:本题考查两角差的余弦公式的应用,同角三角函数的基本关系,以及根据三角函数值求角,注意三角函数值的符号,考查了计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=x2+2x的减区间是( )
| A、(-∞,-1] |
| B、[-1,+∞) |
| C、(-∞,0] |
| D、(-∞,+∞) |
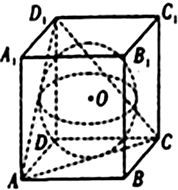 如图,已知球O是棱长为1的正方体ABCD-A1B1C1D1的内切球,则以B1为顶点,以球被平面ACD1截得的圆为底面的圆锥的全面积为
如图,已知球O是棱长为1的正方体ABCD-A1B1C1D1的内切球,则以B1为顶点,以球被平面ACD1截得的圆为底面的圆锥的全面积为
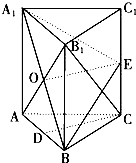 如图三棱柱ABC-A1B1C1中,每个侧面都是正方形,D为底边AB中点,E为侧棱CC1中点,AB1与A1B交于点O.
如图三棱柱ABC-A1B1C1中,每个侧面都是正方形,D为底边AB中点,E为侧棱CC1中点,AB1与A1B交于点O.