题目内容
已知四边形ABCD为正方形，点P为平面ABCD外一点，PD⊥AD，PD=AD=2，∠PDC=60°，则四棱锥P-ABCD的体积为 ．
考点：棱柱、棱锥、棱台的体积
专题：计算题,空间位置关系与距离
分析：确定∠PDC即为二面角P-AD-C为60°，求出棱锥ABCD的底面ABCD上的高，即可求出四棱锥P-ABCD的体积
解答：
解：过P作PE⊥CD
∵ABCD为正方形，PD⊥AD，
∴∠PDC即为二面角P-AD-C为60°，
又∵PD=AD=2
∴PC=2，
则PE=
即为棱锥ABCD的底面ABCD上的高
∴四棱锥P-ABCD的体积V=
S△ABCD•PE=
×4×
=
．
故答案为：
．
∵ABCD为正方形，PD⊥AD，
∴∠PDC即为二面角P-AD-C为60°，
又∵PD=AD=2
∴PC=2，
则PE=
| 3 |
∴四棱锥P-ABCD的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
4
| ||
| 3 |
故答案为：
4
| ||
| 3 |
点评：本题考查四棱锥P-ABCD的体积，考查学生的计算能力，比较基础．
练习册系列答案
全优点练单元计划系列答案
相关题目
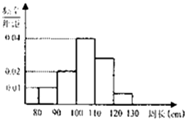为了解一片防风林的生长情况，随机测量了其中100株树木的底部周长（单位：cm）、根据所得数据画出样品的频率分布直方图（如图），那么在这100株树木中，底部周长大于100cm的株数是