��Ŀ����
���ڶ�����Ϊ[0��1]�ĺ���f��x�������ͬʱ������������������
�ٶ������x��[0��1]������f��x����0
��f��1��=1
����x1��0��x2��0��x1+x2��1������f��x1+x2����f��x1��+f��x2�� ������ƺ���f��x��Ϊ���뺯����
����������f��x��Ϊ���뺯������f��0��= ��
�������н�����ȷ���� ����д��������ȷ���۵���ţ�
�ٺ���f��x��=2x-1��x��[0��1]�������뺯����
��������f��x�������뺯�����ٶ�����x0��[0��1]��ʹ��f��x0����[0��1]����f[f��x0��]=x0����f��x0��=x0��
�ٶ������x��[0��1]������f��x����0
��f��1��=1
����x1��0��x2��0��x1+x2��1������f��x1+x2����f��x1��+f��x2�� ������ƺ���f��x��Ϊ���뺯����
����������f��x��Ϊ���뺯������f��0��=
�������н�����ȷ����
�ٺ���f��x��=2x-1��x��[0��1]�������뺯����
��������f��x�������뺯�����ٶ�����x0��[0��1]��ʹ��f��x0����[0��1]����f[f��x0��]=x0����f��x0��=x0��
���㣺�������������
ר�⣺�¶���,���������ʼ�Ӧ��
�������������ȸ������뺯���ĸ�����Բ��ø�ֵ�����ɿ���ȡx1=x2=0������f��x1+x2����f��x1��
+f��x2�����ɵ�f��0����f��0��+f��0��������֪f��0����0���ɵ�f��0��=0��
����Ҫ�жϺ���g��x��=2x-1����x��[0��1]��������[0��1]���Ƿ�Ϊ�����뺯����ֻҪ���麯��g��x��=2x-1���Ƿ��������뺯���������������ɣ�
����������֪���θ�m��n��[0��1]����m��nʱ����m��n֪n-m��[0��1]��f��n��=f��n-m+m����f��n-m��+f��m����f��m�����ɴ��ܹ��Ƶ���f��x0��=x0��������f[f��x0��]=x0����f��x0��=x0��
+f��x2�����ɵ�f��0����f��0��+f��0��������֪f��0����0���ɵ�f��0��=0��
����Ҫ�жϺ���g��x��=2x-1����x��[0��1]��������[0��1]���Ƿ�Ϊ�����뺯����ֻҪ���麯��g��x��=2x-1���Ƿ��������뺯���������������ɣ�
����������֪���θ�m��n��[0��1]����m��nʱ����m��n֪n-m��[0��1]��f��n��=f��n-m+m����f��n-m��+f��m����f��m�����ɴ��ܹ��Ƶ���f��x0��=x0��������f[f��x0��]=x0����f��x0��=x0��
���
�⣺����ȡx1=x2=0������f��x1+x2����f��x1��+f��x2�����ɵ�f��0����f��0��+f��0��
��f��0����0������֪?x��[0��1]������f��x����0�ɵ�f��0����0��
��f��0��=0��
������Ȼf��x��=2x-1��[0��1]������f��x����0����f��1��=1��
��x1��0��x2��0����x1+x2��1��
����f��x1+x2��-[f��x1��+f��x2��]=2x1+x2-1-[��2x1-1��+��2x2-1��]=��2x2-1����2x1-1����0
��f��x��=2x-1���������٢ڢۣ�����f��x��=2x-1Ϊ���뺯����
����������֪���θ�m��n��[0��1]����m��nʱ����m��n֪n-m��[0��1]��
��f��n��=f��n-m+m����f��n-m��+f��m����f��m����
��f��x0����x0����f��x0����f[f��x0��]=x0��ǰ��ì�ܣ�
����f��x0����x0����f��x0����f[f��x0��]=x0��ǰ��ì�ܣ�
��f��x0��=x0��
�ʴ�Ϊ��0���٢ڣ�
��f��0����0������֪?x��[0��1]������f��x����0�ɵ�f��0����0��
��f��0��=0��
������Ȼf��x��=2x-1��[0��1]������f��x����0����f��1��=1��
��x1��0��x2��0����x1+x2��1��
����f��x1+x2��-[f��x1��+f��x2��]=2x1+x2-1-[��2x1-1��+��2x2-1��]=��2x2-1����2x1-1����0
��f��x��=2x-1���������٢ڢۣ�����f��x��=2x-1Ϊ���뺯����
����������֪���θ�m��n��[0��1]����m��nʱ����m��n֪n-m��[0��1]��
��f��n��=f��n-m+m����f��n-m��+f��m����f��m����
��f��x0����x0����f��x0����f[f��x0��]=x0��ǰ��ì�ܣ�
����f��x0����x0����f��x0����f[f��x0��]=x0��ǰ��ì�ܣ�
��f��x0��=x0��
�ʴ�Ϊ��0���٢ڣ�
��������ֵ���ǽ������������ij��÷������������¶�����ת��Ϊ�����������⣬��������ָ�����������ʣ�̽�ֺ����ĺ���ֵ��ָ�������ĵ����Ե�Ӧ�õ�֪ʶ�㣮

��ϰ��ϵ�д�
�����Ŀ
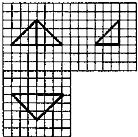 ��ͼ������ֽ��С�����εı߳�Ϊ2������������ij�����������ͼ����˼���������Ϊ
��ͼ������ֽ��С�����εı߳�Ϊ2������������ij�����������ͼ����˼���������Ϊ