题目内容
已知函数f（x）=2cos（2x+
）
（1）当-
≤x≤
时，求函数y=f（x）的最大值和最小值及相应的x的值；
（2）若方程f（x）=a在区间[0，
]上只有一个实数根，求实数a的取值集合．
| π |
| 6 |
（1）当-
| π |
| 6 |
| π |
| 3 |
（2）若方程f（x）=a在区间[0，
| 2π |
| 3 |
考点：余弦函数的图象
专题：三角函数的图像与性质
分析：（1）根据x的范围，利用余弦函数的定义域和值域，求得f（x）的最大值和最小值及相应的x的值．
（2）根据x的范围，利用余弦函数的定义域和值域，求得f（x）的最大值和最小值，从而求得实数a的取值集合
（2）根据x的范围，利用余弦函数的定义域和值域，求得f（x）的最大值和最小值，从而求得实数a的取值集合
解答：
解：（1）当-
≤x≤
时，-
≤2x+
≤
，-
≤cos(2x+
)≤1，
故f（x）最大值为2，此时x=-
，f（x）最小值为-
，此时x=
．
（2）f（x）在区间[0，
]上是减函数，在[
，
]上是增函数，f(0)=
，f(
)=-2，f(
)=0，
所以当a=-2或0＜a≤
时，方程f（x）=a在区间[0，
]上只有一个实数根．
于是满足条件的实数a的取值集合是{a|0＜a≤
，或a=-2}．
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| ||
| 2 |
| π |
| 6 |
故f（x）最大值为2，此时x=-
| π |
| 12 |
| 3 |
| π |
| 3 |
（2）f（x）在区间[0，
| 5π |
| 12 |
| 5π |
| 12 |
| 2π |
| 3 |
| 3 |
| 5π |
| 12 |
| 2π |
| 3 |
所以当a=-2或0＜a≤
| 3 |
| 2π |
| 3 |
于是满足条件的实数a的取值集合是{a|0＜a≤
| 3 |
点评：本题主要考查余弦函数的图象和性质，属于基础题．
练习册系列答案
相关题目
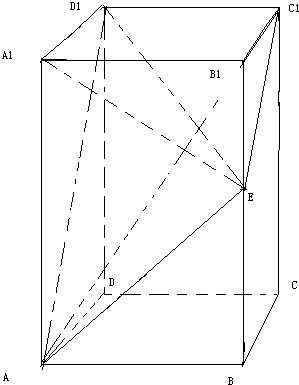长方体ABCD-A1B1C1D1中，AB=AD=1，BB1=2，E为BB1的中点．（1）求证：AE⊥平面A1D1E；
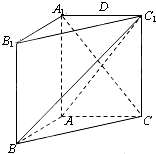如图，在直三棱柱ABC-A1B1C1中，AA1=AC=2AB=2，且BC1⊥A1C．