题目内容
已知曲线C的极坐标方程是ρ=2,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为
(t为参数),则直线l被曲线C截得的线段长为 .
|
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:把参数方程、极坐标方程化为直角坐标方程,再利用点到直线的距离公式、弦长公式求得弦长.
解答:
解:曲线C的极坐标方程是ρ=2,化为普通方程是x2+y2=4,
表示以C(0,0)为圆心、半径等于2的圆.
由
得,x+y-1=0,
则直线l的一般式方程为x+y-1=0,
∴直线l被曲线C截得的线段长为2
=
,
故答案为:
.
表示以C(0,0)为圆心、半径等于2的圆.
由
|
则直线l的一般式方程为x+y-1=0,
∴直线l被曲线C截得的线段长为2
4-(
|
| 14 |
故答案为:
| 14 |
点评:本题主要考查把参数方程、极坐标方程化为直角坐标方程的方法,直线和圆相交时求弦长问题,属于基础题.

练习册系列答案
相关题目
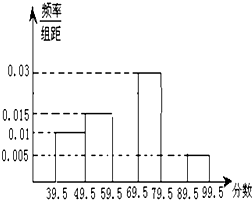 为了解一大片经济林生长情况,随机测量其中的60株的底部周长(单位:cm),规定底部周长60cm及以上优质树木)将周长整理后画出的频率分布表和频率分布直方图如图:观察图形,回答下列问题:
为了解一大片经济林生长情况,随机测量其中的60株的底部周长(单位:cm),规定底部周长60cm及以上优质树木)将周长整理后画出的频率分布表和频率分布直方图如图:观察图形,回答下列问题: