题目内容
设函数f(x)=2lnx-x2.
(1)求函数f(x)的单调递增区间;
(2)若关于x的方程f(x)+x2-x-2-a=0在区间[1,3]内恰有两个相异实根,求实数a的取值范围.
(1)求函数f(x)的单调递增区间;
(2)若关于x的方程f(x)+x2-x-2-a=0在区间[1,3]内恰有两个相异实根,求实数a的取值范围.
考点:利用导数研究函数的单调性,函数的零点
专题:导数的综合应用
分析:求函数f(x)的导数,解f′(x)>0便得增区间.要使关于x的方程f(x)+x2-x-2-a=0在区间[1,3]内恰有两个相异实根,也就是让函数f(x)+x2-x-2-a在[1,3]内有两个零点,令g(x)=f(x)+x2-x-2-a=2lnx-x-2-a,下面要做的就是考查g(x)在区间[1,3]内最值情况,若有最大值,则限制最大值大于0,然后两个端点值都小于0,若有最小值,情况恰好相反.
解答:
解:(1)f′(x)=
,∵x>0,x∈(0,1)时,f′(x)>0,所以函数f(x)的单调递增区间是(0,1].
(2)将f(x)代人方程f(x)+x2-x-2-a=0得2lnx-x-2-a=0,令g(x)=2lnx-x-2-a则g′(x)=
;
∴x∈[1,2)时,g′(x)>0;x∈(2,3]时,g′(x)<0;
∴g(2)是g(x)的极大值,也是g(x)在[1,3]上的最大值;
∵关于x的方程f(x)+x2-x-2-a=0在区间[1,3]内恰有两个相异实根;
∴函数g(x)在区间[1,3]内有两个零点;则有:g(2)>0,g(1)<0,g(3)<0,所以有:
解得:2ln3-5<a<2ln2-4,所以a的取值范围是(2ln3-5,2ln2-4).
| 2(1-x2) |
| x |
(2)将f(x)代人方程f(x)+x2-x-2-a=0得2lnx-x-2-a=0,令g(x)=2lnx-x-2-a则g′(x)=
| 2-x |
| x |
∴x∈[1,2)时,g′(x)>0;x∈(2,3]时,g′(x)<0;
∴g(2)是g(x)的极大值,也是g(x)在[1,3]上的最大值;
∵关于x的方程f(x)+x2-x-2-a=0在区间[1,3]内恰有两个相异实根;
∴函数g(x)在区间[1,3]内有两个零点;则有:g(2)>0,g(1)<0,g(3)<0,所以有:
|
解得:2ln3-5<a<2ln2-4,所以a的取值范围是(2ln3-5,2ln2-4).
点评:利用导数求函数的单调区间,这个不难掌握,注意做第二题g(2)>0,g(1)<0,g(3)<0,这几个限制条件的得出,并掌握做这类题的方法.

练习册系列答案
相关题目
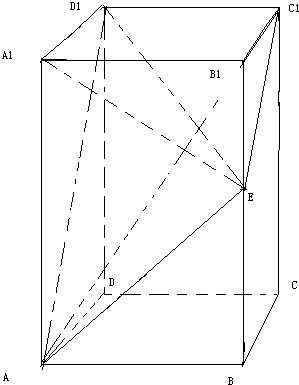 长方体ABCD-A1B1C1D1中,AB=AD=1,BB1=2,E为BB1的中点.(1)求证:AE⊥平面A1D1E;
长方体ABCD-A1B1C1D1中,AB=AD=1,BB1=2,E为BB1的中点.(1)求证:AE⊥平面A1D1E;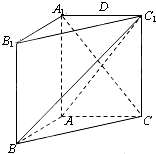 如图,在直三棱柱ABC-A1B1C1中,AA1=AC=2AB=2,且BC1⊥A1C.
如图,在直三棱柱ABC-A1B1C1中,AA1=AC=2AB=2,且BC1⊥A1C.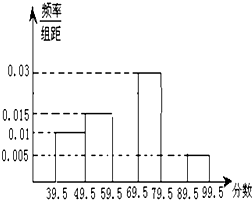 为了解一大片经济林生长情况,随机测量其中的60株的底部周长(单位:cm),规定底部周长60cm及以上优质树木)将周长整理后画出的频率分布表和频率分布直方图如图:观察图形,回答下列问题:
为了解一大片经济林生长情况,随机测量其中的60株的底部周长(单位:cm),规定底部周长60cm及以上优质树木)将周长整理后画出的频率分布表和频率分布直方图如图:观察图形,回答下列问题: