题目内容
1.小王同学有三支款式相同、颜色不同的圆珠笔,每支圆珠笔都有一个与之同颜色的笔帽,平时小王都将笔和笔帽套在一起,但偶尔会将笔和笔帽搭配成不同色.将笔和笔帽随机套在一起,请问小王将两支笔和笔帽的颜色混搭的概率是( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
分析 设三支款式相同、颜色不同的圆珠笔分别为A,B,C,与之相同颜色的笔帽分别为a,b,c,利用列举法求出将笔和笔帽随机套在一起,基本事件有6个,小王将两支笔和笔帽的颜色混搭包含的基本事件有3个,由此能求出小王将两支笔和笔帽的颜色混搭的概率.
解答 解:设三支款式相同、颜色不同的圆珠笔分别为A,B,C,与之相同颜色的笔帽分别为a,b,c,
将笔和笔帽随机套在一起,基本事件有:
(Aa,Bb,Cc),(Aa,Bc,cB),(Ab,Ba,Cc),(Ab,Bc,Ca),(Ac,Bb,Ca),(Ac,Ba,Cb),共有6个基本事件,
小王将两支笔和笔帽的颜色混搭包含的基本事件有:
(Aa,Bc,cB),(Ab,Ba,Cc),(Ac,Bb,Ca),共有3个基本事件,
∴小王将两支笔和笔帽的颜色混搭的概率是p=$\frac{3}{6}=\frac{1}{2}$.
故选:C.
点评 本题考查概率的求法,涉及到古典概型、列举法等基础知识,考查推理论证能力、运算求解能力、数据处理能力,考查数形结合思想、集合思想,是基础题.

练习册系列答案
相关题目
11.函数f(x)的定义域是(0,$\frac{π}{2}$),f′(x)是它的导函数,且f(x)+tanx•f′(x)>0在定义域内恒成立,则( )
| A. | f($\frac{π}{6}$)>$\sqrt{2}$f($\frac{π}{4}$) | B. | $\sqrt{2}$sin1•f(1)>f($\frac{π}{4}$) | C. | f($\frac{π}{6}$)>$\sqrt{3}$f($\frac{π}{3}$) | D. | $\sqrt{2}$f($\frac{π}{4}$)>$\sqrt{3}$f($\frac{π}{3}$) |
16.已知某中学高三文科班学生的数学与地理的水平测试成绩抽样统计如表:
若抽取学生n人,成绩分为A(优秀),B(良好),C(及格)三个等次,设x,y分别表示数学成绩与地理成绩,例如:表中地理成绩为A等级的共有14+40+10=64(人),数学成绩为B等级且地理成绩为C等级的有8人.已知x与y均为A等级的概率是0.07.
(Ⅰ)设在该样本中,数学成绩的优秀率是30%,求a,b的值;
(Ⅱ)已知a≥7,b≥6,求数学成绩为A等级的人数比C等级的人数多的概率.
| 人数 x y | A | B | C |
| A | 14 | 40 | 10 |
| B | a | 36 | b |
| C | 28 | 8 | 34 |
(Ⅰ)设在该样本中,数学成绩的优秀率是30%,求a,b的值;
(Ⅱ)已知a≥7,b≥6,求数学成绩为A等级的人数比C等级的人数多的概率.
10.若函数$f(x)=x(1-\frac{2}{{{e^x}+1}})$则函数f(x)的图象关于( )
| A. | 原点轴对称 | B. | x轴对称 | C. | y轴对称 | D. | y=x对 |
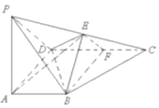 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,CD⊥AD,AD=CD=2AB=2,E,F分别为PC,CD的中点
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB∥CD,CD⊥AD,AD=CD=2AB=2,E,F分别为PC,CD的中点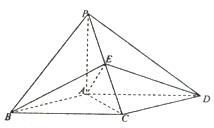 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,AP=AB=AC=a,AD=$\sqrt{2}$a,PA⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,AP=AB=AC=a,AD=$\sqrt{2}$a,PA⊥底面ABCD.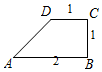 如图,将直角梯形ABCD绕AB边所在的直线旋转一周,由此形成的几何体的体积是$\frac{4π}{3}$.
如图,将直角梯形ABCD绕AB边所在的直线旋转一周,由此形成的几何体的体积是$\frac{4π}{3}$.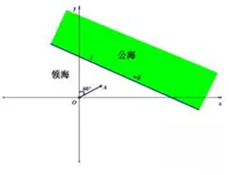 如图,已知直线l:x+$\sqrt{3}$y-c=0(c>0)为公海与领海的分界线,一艘巡逻艇在O处发现了北偏东60°海面上A处有一艘走私船,走私船正向停泊在公海上接应的走私海轮B航行,以使上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,且两者都是沿直线航行,但走私船可能向任一方向逃窜.
如图,已知直线l:x+$\sqrt{3}$y-c=0(c>0)为公海与领海的分界线,一艘巡逻艇在O处发现了北偏东60°海面上A处有一艘走私船,走私船正向停泊在公海上接应的走私海轮B航行,以使上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,且两者都是沿直线航行,但走私船可能向任一方向逃窜.