题目内容
已知函数f(x)=|cosx|-kx在(0,+∞)恰有两个不同的零点α,β(α<β),则下列结论正确的是( )
| A、cosβ=βsinβ |
| B、cosα=αsinα |
| C、cosβ=-βsinβ |
| D、cosα=-αsinα |
考点:函数零点的判定定理,导数的运算
专题:函数的性质及应用
分析:由函数f(x)=|cosx|-kx得到g(x)=|cosx|和函数h(x)=kx,再画出两函数的图象,问题得解.
解答:
解:原题等价于方程|cosx|=kx在(0,+∞)恰有两个不同的解,
等价于函数g(x)=|cosx|与函数h(x)=kx的图象在(0,+∞)恰有两个交点(如图),
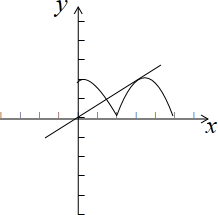
在(
,π)内的交点横坐标为β,且此时直线h(x)=kx与曲线g(x)=|cosx|相切,切点为(β,kβ),
又x∈(
,π)时,g(x)=-cosx,g'(x)=sinx,
故k=g'(β)=sinβ,∴kβ=g(β)=-cosβ.
即cosβ=-βsinβ,
故答案选:C.
等价于函数g(x)=|cosx|与函数h(x)=kx的图象在(0,+∞)恰有两个交点(如图),

在(
| π |
| 2 |
又x∈(
| π |
| 2 |
故k=g'(β)=sinβ,∴kβ=g(β)=-cosβ.
即cosβ=-βsinβ,
故答案选:C.
点评:考查函数零点,导数的应用,解题时可结合图形,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若函数f(x)=
,则函数y=f(x)-x的零点个数是( )
|
| A、0 | B、1 | C、2 | D、3 |
数列{an}为等比数列,若a4=1,a12=16,则a8的值为( )
| A、±4 | ||
| B、-4 | ||
| C、4 | ||
D、4
|
已知集合A={x||x-2|>2},B={x|x∈N},则(∁UA)∩B=( )
| A、{1,2,3} |
| B、{0,1,2,3} |
| C、{0,1,2,3,4} |
| D、{1,2,3,4} |
执行如图所示的程序框图,输出的S的值为( )


| A、0 | ||||
B、
| ||||
| C、1 | ||||
D、
|
已知f(x)=x5+2x3+3x2+x+1,应用秦九韶算法计算x=3时的值时,v3的值为( )
| A、27 | B、11 | C、109 | D、36 |
4名优秀学生A、B、C、D全部都被保送到甲、乙、丙3所学校,每所学校至少去一名,则不同的保送方案共有( )
| A、18种 | B、36种 |
| C、72种 | D、108种 |
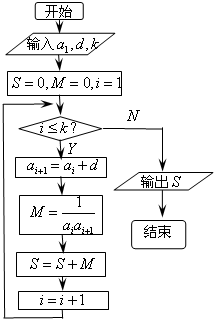 已知数列{an}的各项均为正数,观察程序框图,当k=2时,S=
已知数列{an}的各项均为正数,观察程序框图,当k=2时,S=