Question

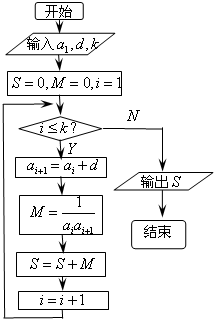已知数列{a_n}的各项均为正数，观察程序框图，当k=2时，S=

2

3

；当k=3时，S=

3

4

．
（1）试求数列{a_n}的通项；
（2）设若[x]表示不大于x的最大整数（如[2.10]=2，[0.9]=0），
求T=[log₂1]+[log₂2]+[log₂3]+…+[log₂（2 an-1）]+[log₂（2 an）]关于n的表达式．

Answer 1

考点：程序框图

专题：计算题,算法和程序框图

分析：（1）根据框图的流程，依次计算k=2，k=3时，输出S的值，利用裂项相消法求得等差数列的首项与公差，可得数列的通项公式；
（2）判断对数值为n-1的对数式的个数为2ⁿ-2^n-1，由此计算T值．

解答： 解：（1）由程序框图知：数列{a_n}的各项均为正数的等差数列，公差为d，
则有

1

akak+1

=

1

d

（

1

ak

-

1

ak+1

）
∴S=

1

d

（

1

a1

-

1

a2

+

1

a2

-

1

a3

+…+

1

ak

-

1

ak+1

）=

1

d

（

1

a1

-

1

ak+1

）
∵若k=2，k=3时，分别有S=

2

3

和S=

3

4

∴

1 d ( 1 a1 - 1 a3 )= 2 3 1 d ( 1 a1 - 1 a4 )= 3 4

解得

a1=1 d=1

或

a1=-1 d=-1

(舍)
故a_n=a₁+（n-1）d=n；
（2）由题意可设T=[log21]+[log22]+[log23]+…[log2(2n-1)]+[log2(2n)]
T=[log21]+[log22]+[log23]+…[log2(2n-1)]+[log2(2n)]
=[log21]+([log22]+[log23])+…+([log2(2k)]+…+[log2(2k+1-1)])+…+[log2(2n)]
=0+1×（2²-2¹）+2×（2³-2²）+…+（n-1）（2ⁿ-2^n-1）+n
=1×2+2×2²+3×2³+…+（n-1）•2^n-1+n
=（n-2）•2ⁿ+n+2．

点评：（1）借助等差数列考查了循环结构的程序框图，根据框图的流程确定k=2，k=3时，输出S的表达式是关键．
（2）考查了数列的求和问题，关键是判断对数值等于n-1的个数．