题目内容
已知函数f(x)=
sinxcosx+cos2x-
(Ⅰ)求函数f(x)的最小正周期T;
(Ⅱ)把f(x)的图象向左平移
个单位,得到的图象对应的函数为g(x),求函数g(x)在[0,
]的取值范围.
| 3 |
| 1 |
| 2 |
(Ⅰ)求函数f(x)的最小正周期T;
(Ⅱ)把f(x)的图象向左平移
| π |
| 12 |
| π |
| 4 |
考点:三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的求值,三角函数的图像与性质
分析:(Ⅰ)由倍角公式化简解析式可得f(x)=sin(2x+
),从而可求最小正周期T;
(Ⅱ)由函数y=Asin(ωx+φ)的图象变换规律先求解析式,即可求函数g(x)在[0,
]的取值范围.
| π |
| 6 |
(Ⅱ)由函数y=Asin(ωx+φ)的图象变换规律先求解析式,即可求函数g(x)在[0,
| π |
| 4 |
解答:
解:(Ⅰ)∵f(x)=
sinxcosx+cos2x-
=
sin2x+
-
=
sin2x+
cos2x
=sin(2x+
),
∴最小正周期T=π;
(Ⅱ)依题意得:g(x)=sin[2(x+
)+
]=sin(2x+
)
∵x∈[0,
],
∴2x+
∈[
,
],
∴sin(2x+
)∈[
,1],
∴g(x)的取值范围为[
,1].
| 3 |
| 1 |
| 2 |
=
| ||
| 2 |
| 1+cos2x |
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
=sin(2x+
| π |
| 6 |
∴最小正周期T=π;
(Ⅱ)依题意得:g(x)=sin[2(x+
| π |
| 12 |
| π |
| 6 |
| π |
| 3 |
∵x∈[0,
| π |
| 4 |
∴2x+
| π |
| 3 |
| π |
| 3 |
| 5π |
| 6 |
∴sin(2x+
| π |
| 3 |
| 1 |
| 2 |
∴g(x)的取值范围为[
| 1 |
| 2 |
点评:本题主要考察了三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换,三角函数的图象与性质,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=cosx,x∈(0,2π)有两个不同的零点x1,x2,且方程f(x)=m(m≠0)有两个不同的实根x3,x4,若把这四个数按从小到大排列构成等差数列,则实数m=( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
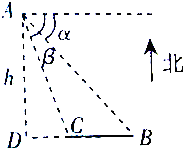 如图,从气球A测得正前方的济南全运会东荷、西柳两个场馆B、C的俯角分别为α、β,此时气球的高度为h,则两个场馆B、C间的距离为( )
如图,从气球A测得正前方的济南全运会东荷、西柳两个场馆B、C的俯角分别为α、β,此时气球的高度为h,则两个场馆B、C间的距离为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图过拋物线y2=2px(p>0)的焦点F的直线依次交拋物线及准线于点A,B,C,若|BC|=2|BF|,且|AF|=3,则拋物线的方程为( )
如图过拋物线y2=2px(p>0)的焦点F的直线依次交拋物线及准线于点A,B,C,若|BC|=2|BF|,且|AF|=3,则拋物线的方程为( )A、y2=
| ||
| B、y2=3x | ||
C、y2=
| ||
| D、y2=9x |